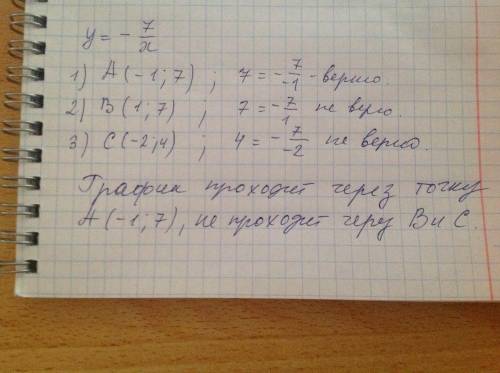

2 см и 2 см
Объяснение:
Дан прямоугольник, периметр которого равен 8 см. Тогда сумма двух сторон равна 8:2 = 4 см. Обозначим через x одну сторону прямоугольника. Тогда вторая сторона равна: 4–x. Теперь составим функцию площади прямоугольника: y=x·(4–x)=4·x-x². Дифференцируем функцию
y'=(4·x–x²)'=4–2·x.
Находим критические точки функции:
y'=0 ⇔ 4–2·x=0 ⇔ x=2 – критическая точка.
Проверим знаки производной:
при x<2: y'=4–2·x>0 и при x>2: y'=4–2·x<0.
Значит, x=2 точка максимума. Тогда
yмакс=y(2)=4·2–2²=8–4=4 см²,
а стороны x=2 см и 4–2=2 см.
1. Перевіримо, чи належить графіку функції точка А(-1;7): якщо х=-1, то у=-7/(-1)=7 - співпало з другою координатою точки (7), отже, через А графік проходить.
2. Перевіримо, чи належить графіку функції точка В(1;7): якщо х=1, то у=-7/1=-7 - не співпало з другою координатою точки (7), отже, через В графік не проходить.
3, Перевіримо, чи належить графіку функції точка С(-2;4): якщо х=-2, то у=-7/(-2)=3,5 - неспівпало з другою координатою точки (4), отже, через С графік непроходить.