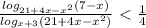
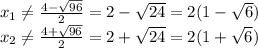
 ) U (
) U ( ; -2) U (-2;
; -2) U (-2;  ) U (
) U ( ; 7).
; 7).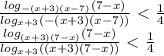
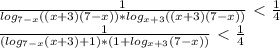
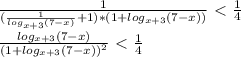
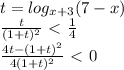
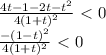
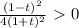
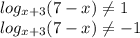
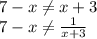
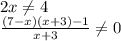
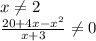
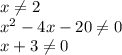
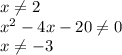
 ) U (
) U ( ; -2) U (-2; 2) U (2;
; -2) U (-2; 2) U (2;  ) U (
) U ( ; 7).
; 7).Тільки по графіку можна одразу вказати, при яких значеннях аргументу значення функції додатні
Приклад: Використовуючи графік функції у = х2 – 1, де -3 ≤ х ≤ 2, знайти значення аргументу, при яких функція набуває додатних значень;
Для значень х таких, що -3 < х < -1, точки графіка розташовані вище осі абсцис. Тому функція набуває додатних значень при -3 < х < -1. Так само вище осі абсцис знаходяться точки графіка для 1 < х < 2. Тому при 1 < х < 2 функція знову набуває додатних значень. Отже, при -3 < х < -1 або 1 < х < 2 функція набуває додатних значень.
(a^2-5a+6)^2+4a^2(5a-6)=a^4+25a^2+36+20a^3-24a^2-10a^3-60a+12a^2=
=a^4+10a^3+13a^2-60a+36=0
a=1; (a-1)^2(a^2+12a+36)=(a-1)^2(a+6)^2
положительный корень один а=1