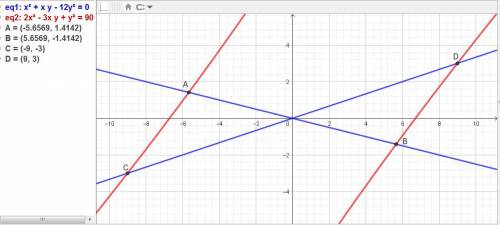
Дана система уравнений:
{x²+xy-12y²=0
{2x²-3xy+y²=90.
Первое уравнение представим так:
x²- (3xy + 4xy) + (-3y*4y) = 0.
Это равносильно разложению на множители:
(x - 3y)(x + 4y) = 0.
Отсюда выразим у = х/3 и у = -х/4, которые подставим во второе уравнение.
Подставим у = х/3.
2x² - 3x(х/3) + (х/3)² = 90,
2x²- x²+ (x²/9)=90,
10x²= 9*90
x = ± 9.
y = ± 9/3 = ± 3.
Найдены 2 корня: х1 = -9, у1 = -3, х2 = 9, у2 = 3.
Подставим у = -х/4.
2x² - 3x(-х/4) + (-x/4)² = 90,
2x²+ (3x²/4)+ (x²/16)=90,
32x² + 12x² + x²= 16*90.
45x²= 16*90
x = √32 = ±(4√2).
y = ± (4√2/4) = ± √2.
Найдены ещё 2 корня: х3 = -(4√2), у1 = √2, х4 = (4√2), у4 = -√2.
ответ: х1 = -9, у1 = -3, х2 = 9, у2 = 3.
х3 = -(4√2), у1 = √2, х4 = (4√2), у4 = -√2.
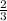от того, что осталось после первого деня, то после второго дня работы осталась 
от того, что осталось после первого дня работы. По условию, после двух дней работы осталось 2 банки, соответственно =2, из чего следует, что во второй день израсходовали 4 банки с краской (так как 2×2=4). По условию сказано, что в первый день израсходовали половину всех банок +1. Значит, 4 банки - это половина всех банок -1. Соответственно, половина - это 4+1=5. В первый день израсходовали 5+1=6 (банок с краской), во второй день израсходовали 4 (банки с краской), а осталось на третий день еще 2 (банки с краской). Суммируем все количество банок: 6+4+2=12.
2) = - 0.126*X^2*Ч
(если вместо Ч стоит Х, то будет (- 0.126X^3)
3) = + 2.4* M^10 *N