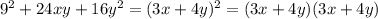
возможно 5 случая:
1) допустим, х-отрицательное, а y положительноетогда сумма (3x+4y) будет отрицательной, а произведение (3x+4y)(3x+4y) будет положительно.(тоже самое будет, если наоборот y-отрицательное, а x положительное)
2) допустим, х и y отрицательные,тогда сумма (3x+4y) будет положительна и произведение (3x+4y)(3x+4y) тоже будет положительно.
3) допустим, х и y положительные, тогда сумма (3x+4y) будет положительна и произведение (3x+4y)(3x+4y) соответственно будет положительно
4) допустим любая из переменных x или y=0, тогда независимо от неравной нулю переменной произведение (3x+4y)(3x+4y) будет положительно
и 5) самый простой случай, когда и х и y =0, тогда и сумма и произведение будут равны нулю, т.е. неотрицательны.
во всех 4х случаях выходит, что выражение неотрицательно, ч.т.д.
y''=4x-2 y''(0)=-2 max x2=1- min
y(0)=0
y(1)=2/3-1=-1/3 y(3)=18-9=9
максимум на отрезке y(3)=9
2) y(-2)=-12/5=-2,4 y(3)=18/10=1,8
6(x^2+1-x(2x))/(x^2+1)^2 1-x^2=0 x=-1 x=1
y'=(1-x^2)/(x^2+1)^2
-1-min
y(-1)=-6/2=-3
минимум на отрезке (-1)=-3
3) y'=-2/x^2+2x^(-3/2) x=1
y(1)=2-4+7=5
maх 7
разность равна 7-5=2
4) a*b=b*(12-2b)=12b-2b^2
12-4b=0 b=3
a=12-6=6
ab=6*3=18