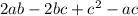
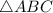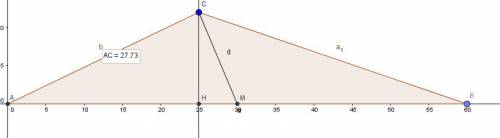
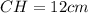. 
— высота, 
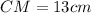— медиана, 
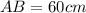— основание. 
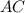— искомая сторона.
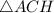— прямоугольный (так как 
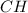— высота по условию), значит можем найти 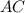по теореме Пифагора, зная 
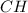и 
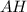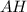. — неизвестная, найдем длину этого отрезка.
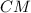— медиана, то есть делит 
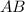пополам: 
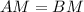. Также нам известна сторона 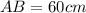. Отсюда: 
. 
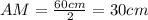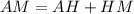(напомню, мы ищем 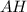). Отсюда 
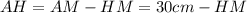. Итак, мы «наткнулись» на еще одну неизвестную — 
. Найдем ее — значит найдем 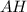. Найдем 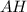— значит найдем 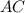.. Из рисунка видно, что 
(эта запись означает, что является частью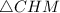 
). Рассмотрим 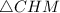. Он прямоугольный, так как 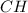— высота по условию. 
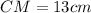— гипотенуза, 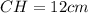— катет. Можем по теореме Пифагора найти :
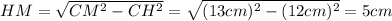
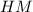нашли. Можем теперь найти :
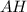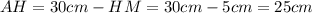
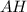, значит можем найти и искомую сторону 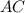по теореме Пифагора: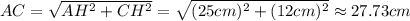
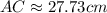
x²=kx+m
x²-kx-m=0
Обозначим дискриминант:
D=k²+4m
а) Чтобы графики не пересекались,дискриминант уравнения x²-kx+m=0
должен быть меньше нуля:
k²+4m<0
Теперь можем брать любые значения k и m ,подходящие условию,например,k=2 и m=-3,получим прямую y=2x-3.
б) Чтобы графики пересеклись дважды,дискриминант уравнения x²-kx+m=0 должен быть больше нуля:
k²+4m>0
Так же берём любые значения k и m,подходящие условию,например,k=4 и m=-2,получим прямую y=4x-2.
в) Чтобы графики пересеклись единожды,то есть прямая коснулась параболы,дискриминант уравнения x²-kx+m=0 должен быть равным нулю:
k²+4m=0
Пусть k=2 и m=-1,получим прямую y=2x-1.