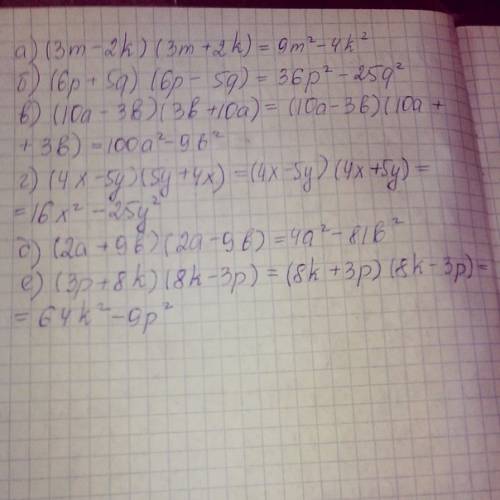
Найдите точку минимума функции
y = x³ - 18x² + 81x + 23
y’ = 3x² - 36x + 81
y’ = 0
3x² - 36x + 81 = 0 / : 3
x² - 12x + 27 = 0
D = b² - 4ac = 144 - 4 * 1 * 27 = 144 - 108 = 36 (6²)
x₁ = (-b-√D)/2a = (12-√36)/2 = 6 : 2 = 3
x₂ = (-b+√D)/2a = (12+√36)/2 = 18 : 2 = 9
+ 3 - 9 + f(x)’
○○...
⬊ max ⬈ min ⬊
Таким образом данная функция имеет минимум в точке 9.
ответ: 9
Найдите точку максимума функции
y = x³ + 4x² + 4x + 17
y’ = 3x² + 8x + 4
y’ = 0
3x² + 8x + 4 = 0
D = b² - 4ac = 64 - 4 * 3 * 4 = 16 (4²)
x₁ = (-b-√D)/2a = (-8-4)/6 = -2
x₂ = (-b+√D)/2a = (-8+4)/6 = -4/6 = -2/3
+ -2 - -2/3 + f(x)’
○○...
⬊ max ⬈ min ⬊
Таким образом максимум функции достигается в точке -2.
ответ: -2
б)=36p^2-25q^2
в)=100a^2-9b^2
г)=16x^2-25y^2
д)=4a^2-81b^2
е)=64p^2-9p^2