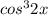Если , то получим линейное неравенство: Полученный промежуток не включает в себя заданыый . Рассматриваем случай, когда - имеем квадратное неравенство. Заданное неравенство ">0", в зависимости от знака старшего коэффициента общие решения неравенства можно записать в виде: - если старший коэффициент больше 0: - если старший коэффициент меньше 0: Вывод: необходимо рассмотреть случай с положительным старшим коэффициентом: , тогда Решаем неравенство. Приравниваем левую часть к нулю: Получившийся дискриминант всегда больше 0, т.к. Чтобы получившийся ответ включал интервал х>3, необходимо потребовать выполнение следующего условия: Так как в рассматриваемом случае , то можно перейти к следующему неравенству: Итоговое решение с учетом рассматриваемого ограничения : Искомое минимальное целое значение ответ: 2
Мне поначалу показалось что речь идет о числе пи, но у этого числа одно значение, поэтому для моего удобства, я вместо п обозначу через букву : Что бы у уравнения было 2 корня, его дискриминант должен быть строго больше нуля. Во первых найдем дискриминант нашего уравнения:
Теперь составим неравенство: Решаем неравенство методом интервалов:
Это и есть ответ. Если вы не поняли что там написано, поясняю: p принадлежит интервалу от (минус бесконечность до -3) символ объединения множеств (и от 3 до + бесконечность)
1)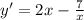
2)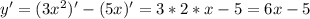
3)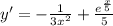
y' = (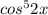 )' = 5*
)' = 5*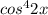 * (-sin2x) *2 = -10 *
* (-sin2x) *2 = -10 *  = -5 * sin4x *
= -5 * sin4x *