1) f(x)=1.2x-10
Линейная функция
область определения R
область значений R
растёт на промежутке (-∞ ; +∞)
не парная не непарная
не переиодичная
точки пересечения с осями
ОХ: 1,2х-10=0
1,2х=10
х=100/12= 8 1/3
ОУ: 1,2*0-10 = -10
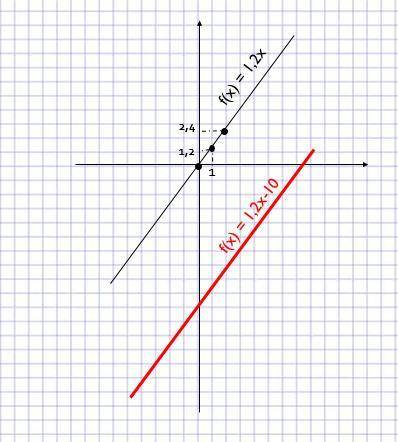
Построим по таблице функцию f(x) = 1.2x и паралельным переносом перенесем по оси ординат на 10 единиц вниз (рисунок 1)
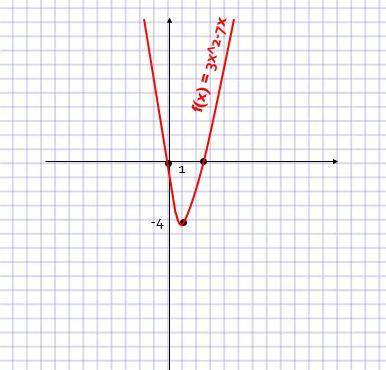
2) 3x^2-7x
Квадратическая функция, графиком которой является парабола
Область определения R
функция ни четная ни нечетная
Область значений y є [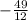
; + ∞)
Ветки вверх , т.к. a больше нуля
Найдем координаты вершины параболы
x0 = -(-7) / 2*3 ≈ 1.1
y0 = 3 *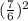 
- 7* 
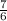= 49/12 - 49/6 = 4 1/12 - 8 2/12 ≈ -4
точки пересечения с осями
С ОХ 3х^2-7x=0
x(3x-7)=0
x1 = 0
x2 = 7/3
С ОУ 3*0^2 - 7*0 = 0
Строим график по данным (рисунок 2)
1) f(x)=1.2x-10
Линейная функция
область определения R
область значений R
растёт на промежутке (-∞ ; +∞)
не парная не непарная
не переиодичная
точки пересечения с осями
ОХ: 1,2х-10=0
1,2х=10
х=100/12= 8 1/3
ОУ: 1,2*0-10 = -10
Построим по таблице функцию f(x) = 1.2x и паралельным переносом перенесем по оси ординат на 10 единиц вниз (рисунок 1)
2) 3x^2-7x
Квадратическая функция, графиком которой является парабола
Область определения R
функция ни четная ни нечетная
Область значений y є [ ; + ∞)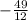
Ветки вверх , т.к. a больше нуля
Найдем координаты вершины параболы
x0 = -(-7) / 2*3 ≈ 1.1
y0 = 3 * 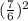- 7* 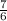= 49/12 - 49/6 = 4 1/12 - 8 2/12 ≈ -4
точки пересечения с осями
С ОХ 3х^2-7x=0
x(3x-7)=0
x1 = 0
x2 = 7/3
С ОУ 3*0^2 - 7*0 = 0
Строим график по данным (рисунок 2)
206
Данные углы - односторонние.
∠АВС+∠BCD=70°+110°=180°
Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180°, эти прямые – параллельны и пересекаться не могут.
Случай 2.
Данные углы - накрестлежащие.
При пересечении параллельных прямых секущей накрестлежащие углы равны. Здесь этого равенства нет. Поэтому в данном случае прямые не параллельны и могут пересечься в некоторой точке К
207
ответьте на вопросы задачи 206, если ∠ABC =65°, a ∠BCD=105
Объяснение: