Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным.
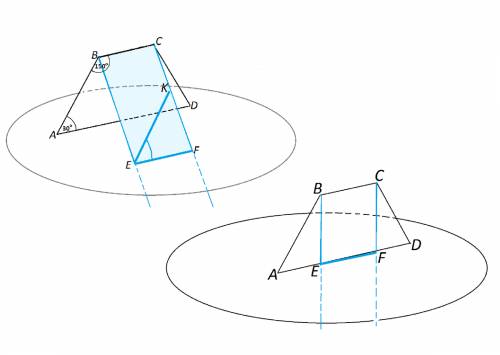
Сумма углов при боковой стороне трапеции 180°, следовательно, угол ВАD=180°-150°=30°.
Проведем в плоскости ВЕF прямую ЕК, параллельную АВ.
ЕК|║АВ; ЕF║АD Углы с соответственно параллельными сторонами равны, если они оба острые или оба тупые.⇒
∠FЕК=∠ВАD=30°
-----------
ВЕ и СF могут быть проведены в плоскости АВСD.
Тогда ЕD будет лежать на АD и в этом случае непараллельные прямые EF и АВ лежат в одной плоскости. Тогда АВ и EF пересекyтся.
a(n) = a1 + d(n - 1)
дано a1 = -1 a7 = -25
a1 = -1
a7 = a1 + d(7 - 1) = -1 + 6d = -25
6d = -24
d = -4
a2 = a1 + d = -1 + (- 4) = -5
a3 = a2 + d = -5 + (- 4) = -9
a4 = a3 + d = -9 + (- 4) = -13
a5 = a4 + d = -13 + (- 4) = -17
a6 = a5 + d = -17 + (- 4) = -21