Объяснение:
Обозначим скорость катера -- х км\ч, скорость течения реки---у км\ч. По течению реки скорость катера будет ( х+у) , против течения ---(х-у) , а в стоячей воде-х. Составим систему согласно условия:
{4(x+y)+3x=148 {5(x-y)-2x=50
{7x+4y=148 {3x-5y=50
Решим систему сложения. Первое уравнение системы умножим на 5, а второе -- на 4 .
35x+20y=740 + {12x-20y=200
47x=940
x=20 скорость катера
Подставим значение х в любое уравнение системы и найдём у:( например , в первое)
7·20+4у=148
140+4у=148
4у=148-140
4у=8
у=2 скорость течения реки
ответ: 20 км\ч ; 2 км\ч
16%
Объяснение:
допустим исходная стоимость товара х
x* 3/5 идет с наценкой 5%. то есть этот товар стал стоить на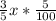
дороже. то есть цена этого товара стала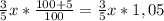 
Осталость 2/5 товара. Половина его, то есть 1/5 продавалась с наценкой 4%, то есть она стоила 1,04x*1/5
Оставшиеся 1/5 товара продавалист с неизвестной наценкой y%, она стоила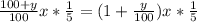
В итоге товар стоил
1,05*x*3/5 + 1,04*x*1/5 + (1+y/100))*x*1/5= (1,05*3+1,04 +(1+y/100)x/5
с другой сторны общая наценка оказалась 7%, то есть товар стал стоить 1,07х
Получаем уравнение
(1,05*3+1,04 +(1+y/100))x/5=1,07х
Сокращаеи на х
(1,05*3+1,04 +(1+y/100))/5=1,07
1,05*3+1,04 +(1+y/100)=1,07*5
3,15+1,04 +1 +y/100=5,35
5,19 +y/100=5,35
y/100=0,16
y=16