Так как площадь ромба равна половине произведения его диагоналей,то найдем вторую диагональ:
Так как диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополям,то по теореме пифагора
пусть ОМ-полудиагональ
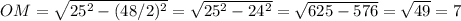 см
см
7*2=14 см-вторая диагональ
Тогда S=48*14/2=336 квадратных сантиметров
ответ:336 см^2
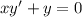
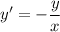 - уравнение с разделяющимися переменными
- уравнение с разделяющимися переменными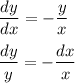
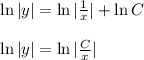
 - общее решение
- общее решение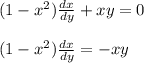

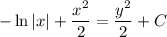 - общий интеграл
- общий интеграл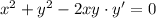

 , тогда
, тогда 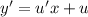



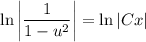
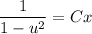
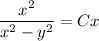 - общий интеграл
- общий интеграл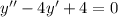
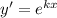 , тогда будем иметь характеристическое уравнение следующего вида:
, тогда будем иметь характеристическое уравнение следующего вида:
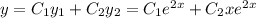 - общее решение
- общее решение
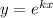 , тогда получаем
, тогда получаем
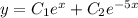

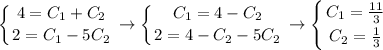
 - частное решение
- частное решение
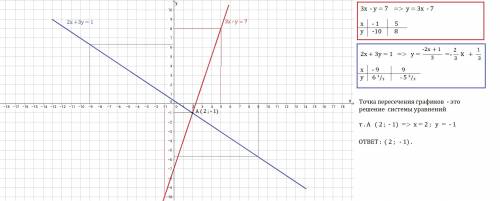
Решение оформлено в виде картинки. При решении использовались следующие характеристические свойства ромба: 1.) Все стороны равны. 2.) Диагонали в точке пересечения делятся пополам.