Исследовать функцию y=-x^4+8x^2-9 и построить ее график.
1. Область определения функции - вся числовая ось.
2. Функция y=-x^4+8x^2-9 непрерывна на всей области определения. Точек разрыва нет.
3. Четность, нечетность, периодичность:
Так как переменная имеет чётные показатели степени, то функция чётная, непериодическая.
4. Точки пересечения с осями координат:
Ox: y=0, -x^4+8x^2-9=0, заменим x^2 = n.
Квадратное уравнение, решаем относительно n:
Ищем дискриминант:
D=8^2-4*(-1)*(-9)=64-4*(-1)*(-9)=64-(-4)*(-9)=64-(-4*(-9))=64-(-(-4*9))=64-(-(-36))=64-36=28;
Дискриминант больше 0, уравнение имеет 2 корня:
n₁=(√28-8)/(2*(-1)) = (√28-8)/(-2) = -(2√7/2-8/2)= 4 -√7 ≈ 1,354249;
n₂ = (-√28-8)/(2*(-1)) = (-2√7-8)/(-2)= 4 + √7 ≈ 6,645751.
Обратная замена: х = √n.
x₁ = √1,354249 = 1,163722, x₂ = -1,163722.
x₃ = √6,645751 = 2,57793, x₄ = -2,577935.
Получаем 4 точки пересечения с осью Ох:
(1,163722; 0), (-1,16372; 0), (2,57793; 0), (-2,57793; 0).
x₃ = √6,645751 = 2,57793,
Oy: x = 0 ⇒ y = -9. Значит (0;-9) - точка пересечения с осью Oy.
5. Промежутки монотонности и точки экстремума:
y=-x^4+8x^2-9.
y'=0 ⇒-4x³+16x = 0 ⇒ -4x(x²-4) = 0.
Имеем 3 критические точки: х = 0, х = 2 и х = -2.
Определяем знаки производной вблизи критических точек.
x = -3 -2 -1 0 1 2 3Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
Минимум функции в точке: x = 0.
Максимумы функции в точках:
x = -2.
x = 2.
Убывает на промежутках (-2, 0] U [2, +oo).
Возрастает на промежутках (-oo, -2] U [0, 2).
6. Вычисление второй производной: y''=-12х² + 16 ,
Найдем точки перегибов, для этого надо решить уравнение
\frac{d^{2}}{d x^{2}} f{\left (x \right )} = 0
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
\frac{d^{2}}{d x^{2}} f{\left (x \right )} = 0
Вторая производная 4 \left(- 3 x^{2} + 4\right) = 0.
Решаем это уравнение
Корни этого уравнения
x_{1} = - \frac{2 \sqrt{3}}{3}.
x_{2} = \frac{2 \sqrt{3}}{3}.
7. Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках [-2*sqrt(3)/3, 2*sqrt(3)/3]
Выпуклая на промежутках (-oo, -2*sqrt(3)/3] U [2*sqrt(3)/3, oo)
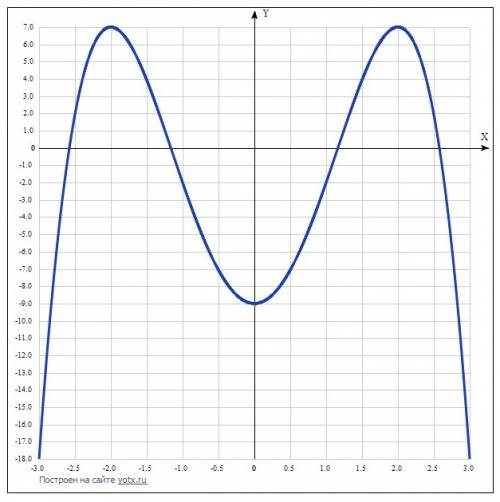
8. Искомый график функции в приложении.
1) Выделяем полные квадраты:
для y: (y²+2*7y + 72) -1*72 = (y+7)²-49
Преобразуем исходное уравнение:
(y+7)² = 6x - 0
Получили уравнение параболы:
(y - y0)² = 2p(x - x0)
(y+7)² = 2*3(x - 0)
Ветви параболы направлены вправо, вершина расположена в точке (x0, y0), т.е. в точке (0;-7)
Параметр p = -3.
Координаты фокуса: F(-p/2; yo) = (-1,5; -7).
Уравнение директрисы: x = x0 - p/2
x = 0 - 3/2 = -3/2.
2) Выделяем полные квадраты:
для x: (x²-2*1x + 1) -1 = (x-1)²-1
для y: -4(y²+2*3y + 3²2) +4*3² = -4(y+3)²+36
В итоге получаем:
(x-1)²-4(y+3)² = -68
Разделим все выражение на -68
(-1/68)(x - 1)² + (1/17)(y + 3)² = 1.
Параметры кривой.
Данное уравнение определяет гиперболу с центром в точке:
C(1; -3)
и полуосями: a = 2√17, b =√17.
Найдем координаты ее фокусов: F1(-c;0) и F2(c;0), где c - половина расстояния между фокусами
Определим параметр c: c² = a² + b² = 68 + 17 = 85
c = √85.
Тогда эксцентриситет будет равен: e = c/a = √85/2√17.
Асимптотами гиперболы будут прямые: y + 3 = (1/2)(x - 1) и
y + 3 = (-1/2)(x - 1).
Директрисами гиперболы будут прямые: +-е/а = +-(√68/√85).
= - X^2 + 4X - 3
терерь можно и разложить:
D = 16 - 4*(-1)*(-3) = 16 - 12 = 4
X1 = ( - 4 + 2) \ - 2 = - 2 \ - 2 = + 1
X2 = - 6 \ - 2 = + 3
ответ: - X^2 - 4X + 3 или = (Х - 1)*(X - 3)