ответить на вопросы по теории вероятности: 1. формула полной вероятности : а) пересчитывать имеющиеся доопытные вероятности гипотез н1, , когда становится известно, что произошло некоторое событие а. б) вычислить
вероятность произведения событий, когда известны вероятности отдельных событий. в) вычислить вероятность события а, если известны вероятности всех гипотез и вероятности события а, при условии выполнения каждой
из гипотез. г) находить точечную оценку неизвестной вероятности события а. 2. какие значения может принимать случайная величина имеющая стандартное нормальне распределение? : а) только положительные значения б)
любые действительные значения в) только неотрицательные значения г) только значения из промежутка [-1; 1] 3. среднее арифметическое значений веса студентов, измеренных при едицинском обследовании, при увеличении
числа обследованных : а) имеет распределение вероятностей, мало отличающееся от нормального распределения б) имеет распределение вероятностей, мало отличающееся от экспоненциального распределния в) имеет
распределение вероятностей, мало отличающееся от равномерного распределения г) имеет распределение вероятностей, мало отличающееся от распределения пуассона

👇

Открыть все ответы

Ответ:

artemkafire2005

29.12.2020

1) Возьмём числитель первой дроби за X. Тогда знаменатель будет равен X+3. Первая дробь будет равна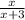 $\frac{x}{x+3}$ Если увеличить числитель первой дроби на два и знаменатель на четыре, то вторая дробь будет равна 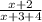$\frac{x+2}{x+3+4}$ В условии задания сказано, что вторая дробь больше первой на 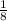$\frac{1}{8}$ , значит разность второй и первой дроби будет равна одной восьмой. Составим уравнение.

$\frac{x+2}{x+7}$ - $\frac{x}{x+3}$ = $\frac{1}{8}$ Чтобы избавиться от дробей умножаем каждое число на (x+7)·(x+3)·8

(x+2)·(x+3)·8 - x·(x+7)·8=(x+7)·(x+3)

(x²+3x+2x+6)·8 - (x²+7x)·8=(x+7)·(x+3)

8x²+24x+16x+48-8x²-56x=x²+3x+7x+21 Переносим всё в левую сторону и приравниваем выражение к нулю. Упростив, получим:

-x²-26+27=0

D=676+108=784;28²

D>0

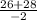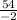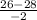x1= $\frac{26+28}{-2}$ = $\frac{54}{-2}$ = -27

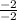x2= $\frac{26-28}{-2}$ = $\frac{-2}{-2}$ =1

Так как у нас получилось два корня, нужно подставить получившиеся значение в исходное выражение и найти верный ответ.

а) Возьмём первый корень, равный -27 и подставим в изначальное выражение.

$\frac{x+2}{x+7}$ - $\frac{x}{x+3}$ = $\frac{1}{8}$

$\frac{-27+2}{-27+3+4}$ - $\frac{-27}{-27+3}$ = $\frac{1}{8}$

$\frac{-25}{-20}$ - $\frac{-27}{-24}$ = $\frac{1}{8}$

$\frac{25}{20}$ - $\frac{27}{24}$ = $\frac{1}{8}$

$\frac{5}{4}$ - $\frac{27}{24}$ = $\frac{30}{24}$ - $\frac{27}{24}$ = $\frac{3}{24}$

$\frac{3}{24}$ = $\frac{1}{8}$ ⇒ Корень -27 подходит. Значит изначальная дробь равна $\frac{27}{24}$ = $\frac{9}{8}$ =1 $\frac{1}{8}$

б) Возьмём второй корень, равный 1 и подставим в изначальное уравнение

$\frac{x+2}{x+7}$ - $\frac{x}{x+3}$ = $\frac{1}{8}$

$\frac{1+2}{1+7}$ - $\frac{1}{1+3}$ = $\frac{1}{8}$

$\frac{3}{8}$ - $\frac{1}{4}$ = $\frac{1}{8}$

$\frac{3}{8}$ - $\frac{2}{8}$ = $\frac{1}{8}$ ⇒ Корень 1 также подходит. Значит исходное уравнение равно $\frac{1}{4}$

Так как при проверке оба корня оказались верны, то в ответе будет две дроби.

2) $\left[\begin{array}{ccc}S&U&t\\200&x&\\200&x+10&\end{array}\right]$

Рассмотрим движение машины в двух случаях: Как она должна была двигаться изначально и как она двигалась в итоге. Путь, пройденный автомобилем, не изменился. Скорость увеличилась на 10 км/ч. Так как автомобиль прибыл быстрее запланированного, то разница между временем, затраченным в первом случае, и временем, затраченным во втором случае, будет равна 1 часу. Составим уравнение.

$\frac{200}{x}$ - $\frac{200}{x+10}$ =1 Избавимся от дробей, умножив каждое число на x·(x+10)