Пётр+Владимир работают с производительностью 22/40, Михаил+Пётр с производительностью 30/50, Владимир+Михаил с производительностью 41/60. Значит, работая вместе:
Пётр+Владимир+Михаил+Пётр+Владимир+Михаил = 22/40 + 30/50 + 41/60, решаем = 110/60 = 11/6. т.е. 11 ящиков за 6 минут. А нам надо 22 ящика, увеличиваем дробь в 2 раза, получаем 22/12. Но это работали 2 Петра, 2 Владимира и 2 Михаила.
Соответственно Петр, Владимир и Михаил перенесут 22 ящика не за 12 мин., а в 2 раза больше, т.е. за 24 мин.
1) tga=y'(x) в некоторой точке, поэтому найдем абсциссу точки касания. Точка пересечения с осью абсцисс имеет y=0, т.е.
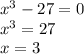
Найдем производную функции в точке с х=3
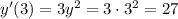
ответ: tga=27
2) функция прерывна в точках в которых производная не определена
найдем производную функции
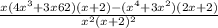
Производная неопределена если ее знаменатель будет равен 0. Найдем эти значения
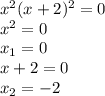
эти значения разбивают числовую прямую на промежутки непрерывности
(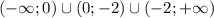
3) скорость точки это производная f'(x) уравнения движения, а ускорение - это производная от скорости движения или вторая производная f"(x) уравнения движения в заданной точке. Надем скорость
V(1)=f'(1)=12-6t=12-6*1=6
a(1)=V'(1)=(12-6t)'=-6
4) уравнение касательной к графику функции y = f(a) + f '(a)(x – a)
f(-3)=2-(-3)^2=2-9=-7
f'(-3)=-2x=-2*(-3)=6
y=-7+6(x+3)
y=6х+11 (рисунок не могу здесь выполнить)
5) задание не полное.
Объяснение:
f(x)=x²-8x
найдем экстремумы
f'(x)=2x-8=0 ; 2(x-4)=0 ; x=4
на отрезке [-2;1] экстремумов нет . тогда наименьшее значение функции надо найти на концах отрезка
f(-2)=(-2)²-8(-2)=4+16=20
f(1)=1²-8*1=1-8=-7
ответ. Наименьшее значение функцииf(x)=x²-8x на отрезке[-2;1] -7