Исследуйте на четность функцию :
1) y = f(x) = - 8x + x² + x³
2) y = f(x) = √(x³ + x²) - 31*| x³ |
ни четные ,ни нечетные
Объяснение:
1)
f(x) = - 8x + x² + x³ ; Область Определения Функции: D(f) = R
функция ни чётная ,ни нечётная
проверяем:
Функция является четной, когда f(x)=f(-x) , нечетной, когда f(-x)=-f(x)
а) f(-x) = - 8*(-x) +(- x)² +(- x)³ = 8x + x² - x³ ≠ f(-x)
Как видим, f(x)≠f(-x), значит функция не является четной.
б)
f(-x) ≠ - f(-x) → функция не является нечетной
- - - - - -
2)
y = f(x) = √(x³ + x²) - 31*| x³ | ,
D(f) : x³ + x² ≥ 0 ⇔ x²(x+1) ≥ 0 ⇒ x ≥ -1 * * * x ∈ [ -1 ; ∞) * * *
ООФ не симметрично относительно начало координат
* * * не определен , если x ∈ ( -∞ ; - 1) * * *
функция ни чётная ,ни нечётная
Все в объяснениях.
Объяснение:
1. Постройте график функции y=f(x).
Гипербола, полученная сдвигом графика у=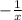
на 1 вверх по оу. у(-2)=0,5 ;у(-1)=1 ;у(-2)=0,5 ;у(2)=-0,5 ;у(1)=-1 ;у(2)=-0,5
2. f '(x)= (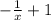
) ' =
.
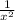3. Уравнения касательной y =к (x −x₀)+f (x₀) .
Прямая y=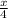
, к=1\4.
Найдем точку касания
(x-2)²=0 , x=2.
f (2)=-1\2+1=0,5
y =0,25* (x −2)+0,5
у=0,25х
Вторая касательная пройдет через х=-2
f (-2)=1\2+1=1,5
y =0,25* (x −2)+1,5
у=0,25х+1
4. Наименьшее значение функции у'=(x−f(x) ) '=(х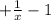
)' =
=1 -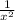
=
.
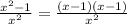у'=0 ,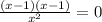
,х=1 , х=-1.
На промежутке [1/2;∞) лежит только х=1
у'______[1\2] - - - - -(1)+ + + + +
y ↓ ↑
x=1 точка минимума.
Наименьшее значение может быть при х=1\2 или х=1:
у(1\2) =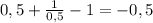
.
у(1)= 1+1-1=1.
Наименьшее значение функции х-f(x) равно -0,5