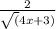ответ: (0;2) и (1,5; 1,3)
Решение: 1) Уравнение х²+у²=4 преобразуем в виде х²+у²=2², это уравнение окружности с центром в начале координат и радиса R=2. 2) Построим координатную плоскость, на ней с циркуля или от руки построим окружность с цетром в начале координат и радиуса 2 клетки. 3) Преобразуем уравнение у=х²-2х+2 = х² -2х +1 +1= ( х² -2х +1 )+ 1 = (х - 1)²+1 . Графиком уравнения у=(х - 1)²+1 является парабола с вершиной в точке (1; 1). Построим параболу на той же координатной плоскости, задав несколько точек: 1 точка-если х=0, то у=2; 2 точка- если х=1, то у=1; 3 точка= если х=2, то у=2; 4 точка- если х= -1, то у=5; 5 точка- если х=3, то у=5. 4) Парабола и окружность пересекаются в двух точках, отметим их на рисунке и найдём координаты: (0; 2) и (1,5 ; 1,3)
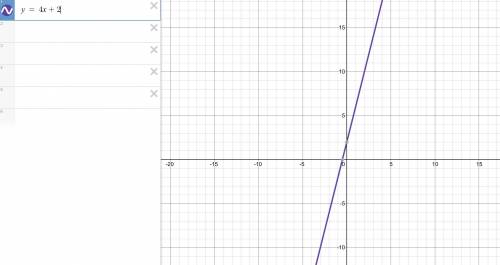
B1: y = 4x + 2
B4: (x - 4)² + (y - 3)² = 25
С2: h = 15/√34
Объяснение:
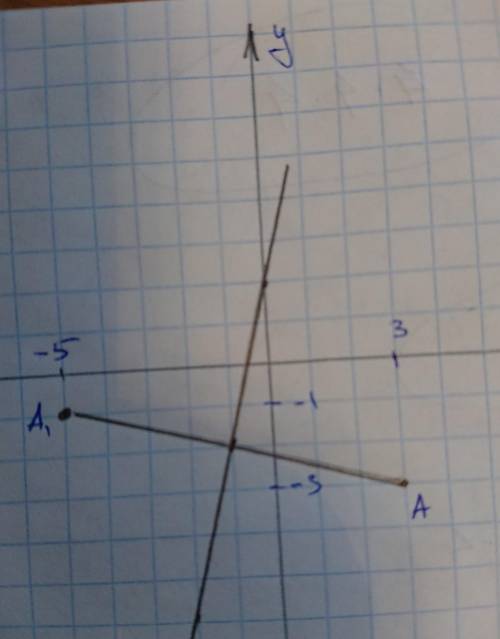
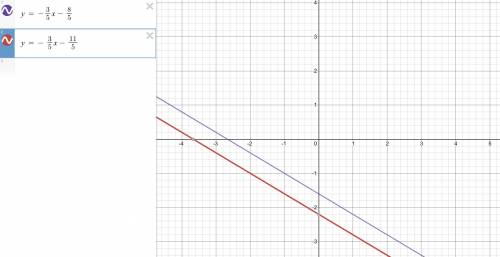
B1: Прямая проходящая через A1 и A имеех наклон Δy/Δx = -2/8 = -1/4 => k1 = -1/4
Значит k перпендикулярной прямой будет k = -1/k1 = 4
Искомая прямая должна проходить через середину отразка, соединяющего A1 и A. Это т. (-1; 2) => y = 4x + 2
см. рисунок и фото.
B4:
x² + y² + 6x - 8y = 0
Преобразуем:
(x² + 6x + 9) + (y² - 8y + 16) - 9 - 16 = 0
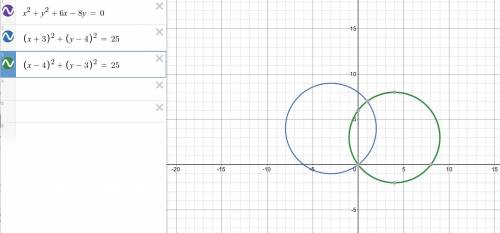
(x + 3)² + (y - 4)² = 25
Это окружность с центром в точке (-3; 4) и радиусом 5
Поворот на 270° против часовой равен повороту на 90° по часовой. Значит нужно найти урванение для окружности с центром (4; 3) и радиусом 5.
Такое уравнение: (x - 4)² + (y - 3)² = 25.
см. рисунок
С2: см рисунок.
Легко видеть, что расстояние между прямыми это выстота прямоугольного треугольника с катетами a = 3 и b = 5. По т. Пифагора гипотенуза c = √34
S = (1/2)*h*c
S = (1/2) a * b => h = a*b/c = 15/√34
Производная выражения. находящегося по знаком радикала, равна 1 делённоё на два таких выражения, в соответствии с этим получим производную:
y' = 1/2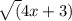 * 4, мы умножили данное значение на 4, так как данная функция является сложной и мы ещё должны найти производную функции, находящейся под знаком радикала.
* 4, мы умножили данное значение на 4, так как данная функция является сложной и мы ещё должны найти производную функции, находящейся под знаком радикала.
Запишем полный ответ: y' =