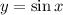и 
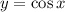равен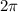 
. При этом функции вида 
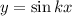и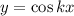 
имеют период 
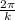. Домножение всей функции на постоянный множитель или прибавление константы к переменной под знаком тригонометрической функции либо ко всей функции не меняет ее период: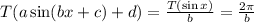 
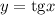и 
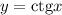равен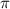 
, а функций 
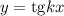и 
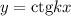равен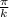 
.
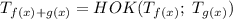
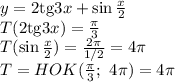
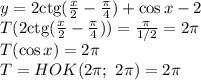
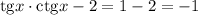
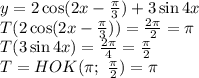
(х + 54) - скорость второго автомобилиста на второй половине пути
примем за 1 длину всего пути, 1/2 - половина пути, тогда
1/х - время, затраченное первым автомобилистом на весь путь
1/2 : 36 = 1/72 - время, затраченное вторым автомобилистом на первую половину пути
1/2 : (х + 54) = 1/(2(х + 54)) - время, затраченное вторым автомобилистом на вторую половину пути
Уравнение
1/х = 1/72 + 1/(2(х + 54))
72* (x + 54) = x * (x + 54) + x * 36
72x + 3888 = x² + 54x + 36x
х² + 18х - 3888 = 0
D = 18² - 4 * 1 * (- 3888) = 324 + 15552 = 15876
√D = √15876 = 126
х₁ = (- 18 + 126) /2 = 108/2 = 54 км/ч - искомая скорость первого
х₂ (-18 - 126) / 2 = - 144/2 = - 72 отрицательное значение не удовлетворяет условию