Пусть, в январе : первая бригада изготвила x деталей , вторая y. в феврале : первая изготовила x+x*40/100 =1,4x деталей ,вторая y -y*10/100 =0,9y {x+y =120 ; 1,4x -0,9y =30. {x+y =120 ; 14x -9y =300. 9(x+y) +(14x-9y) =9*120 +300; 23x =1380 ; x=60 ⇒y =120 -60 =60 x=60 ; y=60.
можно с только одной переменной в январе : первая x , вторая (120 - x). в феврале : : первая 1,4x , вторая 0,9(120 - x) . По условию в феврале разность изготовленных изделий первой и второй бриг составляет 30. 4x -0,9(120 - x) =30; 14x -9(120-x)=300; 14x -1080 +9x =300; 14x =1080+300; x=1380/23=60.
1)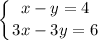
Система решений не имеет, так как отношения коэффициентов при переменных равны, но не равны отношению свободных членов.
--------------------------------------------------------------
2)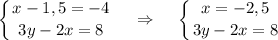
3y = 8 + 2·(-2,5); 3y = 3; y = 1
Система имеет единственное решение ( -2,5; 1)
Если предположить, что в условии опечатка : в первом уравнении потеряна переменная y, тогда система имеет вид
В таком виде система имеет бесконечно много решений, так как отношения коэффициентов при переменных равны отношению свободных членов.
Решения системы можно записать в виде (1,5y-4; y)
--------------------------------------------------------------
3)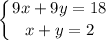
Система имеет бесконечно много решений, так как отношения коэффициентов при переменных равны отношению свободных членов.
Решения системы можно записать в виде (x; 2-x)