Объяснение:
Построить график функции
у=2×|х|+3
Шаг 1.
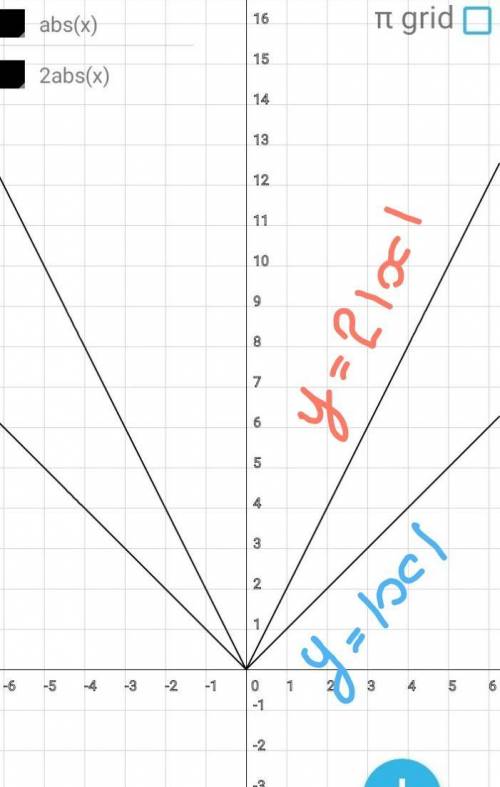
Строим график функции
у=|х|
Графиком являются биссектрисы
1 и 2 координатных четвертей.
Весь график расположен в верхней
полуплоскости.
Шаг 2.
Нужно изменить угол наклона вет
вей графика.
Построим и заполним таблицу:
у=2×|х|
х 0 -2 2
у 0 4 4
Строим график фунеции
у=2×|х|.
Шаг 3.
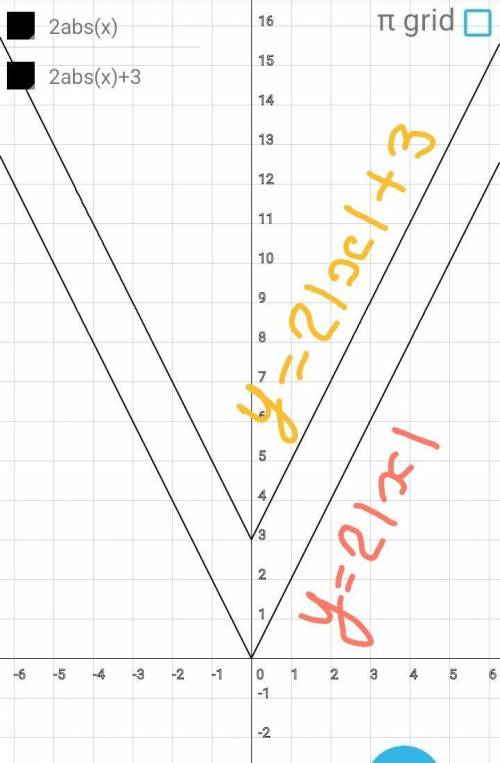
Строим график функции
у=2×|х|+3
График функции у=2×|х| поднимаем
вверх на 3 единицы ( совершаем па
раллельный перенос вдоль положи
тельного направления ОУ на 3ед. от
резка).
Построен искомый график.
Объяснение:
Степень одночлена
Что такое степень одночлена? Как ее найти?
Определение.
Степенью одночлена называют сумму показателей степеней всех входящих в него переменных.
Если одночлен не содержит переменных (то есть является числом), то его степень считают равной нулю.
Таким образом, чтобы найти степень одночлена, надо определить показатель каждой из входящих в него переменных, и сложить их.
Примеры.
\[1)\frac{2}{{15}}a{b^2}{c^4}\]
Показатель a равен 1, показатель b — 2, показатель c — 4. Степень одночлена равна сумме этих показателей: 1+2+4=7.
\[2)xyz\]
1+1+1=3. Следовательно, степень этого одночлена равна 3.
\[3)12,5m\]
степень данного одночлена равна 1.
\[4) - 0,125{a^5}{c^{10}}{p^2}\]
5+10+2=17. Значит, это — одночлен 17-й степени.
\[5)24\]
Одночлен не содержит переменных. По определению, степень такого одночлена равна нулю.
Пусть в первом городе х тогда во втором 2х в тертьем 2х-400 *уровнение*
х+2х+2х-400=6000 : 5х-400=6000 : 5х=6000 : х= 6400/5 : х = 1280 а дальше умножаем на два така как в два раза больше а третье ко второму прибовляем 400