Я же написал ответ. Зачем извращать. Рассуждения примитивные, без использования формул и определенийЮ чтобы было понятно всем.
На 1 должность 25 кандидатов
на 2 24
на 3 23
на 4 22, потому что разные должности - разные люди, а так как эти выборы независимы, получаем общее количество вариантов
25*24*23*22.
1. Уравнение можно решить так же, как это сделал(а) Agnesmile02464, но можно ещё сделать через дискриминант.
x^2 - 6x - 7 = 0
D = b^2 - 4ac;
D = -6^2 - 4 * 1 * (-7) = 36 + 28 = 64
x = (-b +-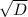 
)/2a
x1 = (6 +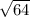 
)/2 * 1 = (6 + 8)/2 = 14/2 = 7
x2 = (6 - 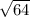)/2 * 1 = (6 - 8)/2 = -2/2 = -1
2. Для решения этого задания есть специальная формула, но я её благополучно забыл.) Попробую решить через систему. Для решения этого задания нам понадобится всеми любимая формула y=kx + b. Нужно взять две любые точки, через которые проходит прямая, и подставить. Получаем:
(-1;3) и (1;-3)
Подставляем в формулу, получаем систему:
{3 = -k + b
{-3 = k + b
Перенесем значения, чтобы были легче:
{k - b = -3
{-k - b = 3
Нам нужно найти k и b. Отнимем эти уравнения, чтобы избавиться от b и, для начала, найти k:
k - b - (-k) - (-b) = -3 - 3
k - b + k + b = -6
2k = -6
k = -3
Подставим в саааамое первое уравнение:
3 = - (-3) + b
3 = 3 + b
-b = 3 - 3
b = 0
k = -3, b = 0. Подставляем значения в y = kx + b и получаем функцию:
y = -3x
ответ 1)
Объяснение: Если что-то непонятно - не стесняйся и спрашивай ;)
Не знаю, правильно или нет, но только это в голову лезит.
Всего 25 учеников и 4 должности.
Представим, что у нас 25 учеников и 1 должность - тогда вариантов 25, а т.к должностей 4 - то 25*4 = 100. Эти 100 вариантов будут приходиться на 1 ученика.
А всего учеников 25, следовательно 25*100 = 2500
ответ