

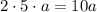
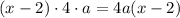

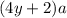 . По условию она увеличилась в k раз. Получаем равенство:
. По условию она увеличилась в k раз. Получаем равенство: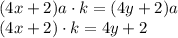
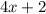 и выражение
и выражение 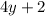 при делении на 4 дает остаток 2. Однако при четном
при делении на 4 дает остаток 2. Однако при четном  возникает противоречие:
возникает противоречие:
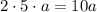
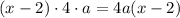

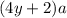 . По условию она увеличилась в k раз. Получаем равенство:
. По условию она увеличилась в k раз. Получаем равенство: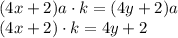
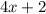 и выражение
и выражение 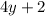 при делении на 4 дает остаток 2. Однако при четном
при делении на 4 дает остаток 2. Однако при четном  возникает противоречие:
возникает противоречие: