a > b и b < a
Объяснение:
Решение на фото, на всякий случай продублирую, если будет не видно.
Неверные неравенства:
a > b и b < a
Представим, что точка А это -2 (можно брать и -1, результат будет таким же). Точка b - это +1
Исходя из этого решаем:
1)b> a
1 > -2 - верно, т.к положительное число больше отрицательного;
2) a + 10 < b + 10
-2 + 10 < 1 + 10
8 < 11 - верно;
3) a < 0
-2 < 0 - верно, т.к отрицательное число меньше нуля;
4) a > b
-2 > 1 - неверно, т.к положительное число больше отрицательного
-2 < 1 - верно
5) b < a
1 < -2 - неверно, т.к положительное число больше отрицательного
1 > -2 - верно
1) 1-3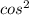
x=2sin(x)cos(x)
единицу представим по тригонометрическому тождеству:1=sin²x+cos²x
sin²x+cos²x-3cos²x-2sin(x)cos(x)=0
sin²x-2sin(x)cos(x)-2cos²x=0
делим каждый член уравнения на cos²x
tg²x-2tgx-2=0
решаем квадратное уравнение
D=12
tgx₁=1+√3 tgx₂=1-√3
x₁=arctg(1+√3)+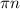
x₂=arctg(1-√3)+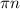
2) 3Sin²x+2SinxCosx=2
3Sin²x+2SinxCosx=2(Sin²x+Cos²x)
Sin²x+2SinxCosx-2Cos²x=0
Уравнение однородное 2 степени. Разделим его на Cos²x
Tg²x+2Tgx-2=0
Tgx=y
y²+2y-2=0
D=12>0
y=(-2+2√3)/2=-1+√3 или y=(-2-2√3)/2= -1-√3
Tgx=-1+√3⇒ x=arctg(-1+√3)+πn,n∈Z
Tgx= -1-√3 ⇒x= arctg(-1-√3)+πn,n∈Z
3(3b-8) вроде так А второй я не знаю