
Пусть первое число - x, второе - y, третье - z.
По условию задачи x+y+z = 35. В то же время, эти числа являются членами геом.прогрессии, т.е. y/x = z/y = q (знаменатель прогрессии). Если первое число увеличить на 2, второе оставить без изменений, а третье уменьшить на 7, то получится арифметическая прогрессия. То есть y-(x+2) = (z-7)-y = d (разнать прогрессии). Получаем систему из трёх уравнений с тремя неизвестными:
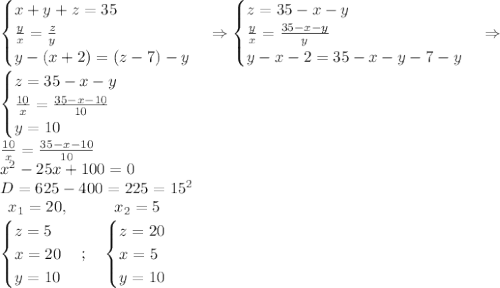 .
.
Это либо члены геом.прогрессии 20, 10, 5 со знаменателем 0,5, либо 5, 10, 20 со знаменателем 2.
Пусть x г. - первоначальная масса раствора.
(30/x)*100 процентов соли в растворе
(x+100) после добавления воды.
(30/(x+100))*100 Концентрация соли после добавления воды.
Так как в результате, концентрация соли в растворе понизилась на 1%, то уравнение.
((30/x)*100)-(30/(x+100))*100=1
(3000/x)-(3000/(x+100))=1
300000/x(x+100)=1
300000=x^2+100x
x^2+100x-300000=0
D=100^2-4*(-300000)=10000+1200000=1210000
x1=(-100+1100)/2=1000/2=500
x2=(-100-1100)/2=-1200/2=-600 - не подходит
ответ: 500 г. первоначальная масса раствора