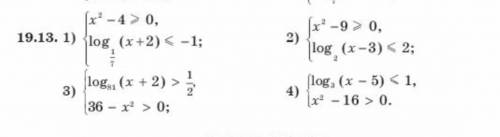
Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
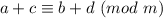
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
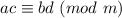
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
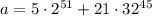
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например, 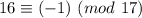 , но сейчас это не нужно), нам повезло, это 32
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что 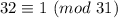 , получаем
, получаем
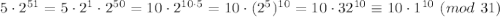
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
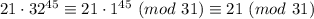
Остаток 21, чудесно. Выполняем последний шаг.
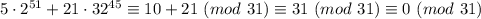
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
1. -1,4
2. Одночленом не является то выражение, части которого не разделяются плюсом или минусом (К примеру, 2abc будет одночленом, а ab + 2c не будет, в общем, ab + 2c будет многочленом), в данном случае ответом будет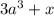
3. Подобные слагаемые - те, которые имеют одну и ту же буквенную часть (Если одна буква возведена в одну степень, а другая в другую, они не будут подобными слагаемыми), при выполнении действий с ними, коэффициенты (Числа перед буквами) слагаются/вычисляются, в данном случае ответом будет 3a + 4b
4. При умножении одинаковых переменных степени слагаются, т.е., в данном случае будет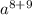 =
= 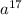
5.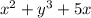 , как решать, я уже объяснял
, как решать, я уже объяснял
6. 4y + 5 (8y - (4y - 5) = 8y - 4y + 5, так как перед скобкой стоит минус, остальное я уже объяснял)
7. 16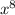 , так как, если после скобок стоит степень, степени внутри скобок умножаются на степень после скобок
, так как, если после скобок стоит степень, степени внутри скобок умножаются на степень после скобок
8. 12x - 14 (Просто число перед скобками умножается на числа внутри скобок)
9.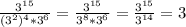 (В конце степени просто сокращаются, и остается только 3)
(В конце степени просто сокращаются, и остается только 3)
10.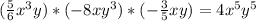 (Коэффициенты сокращаются, и в итоге остается
(Коэффициенты сокращаются, и в итоге остается 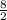 , что равно 4, а результат положительный, так как отрицательное число, умноженное на отрицательное, становится положительным)
, что равно 4, а результат положительный, так как отрицательное число, умноженное на отрицательное, становится положительным)