пусть время отправления поезда будет х часов. если он будет идти со скростью 4 км/ч , то он затратит х + 0.5 (30 мин = 0.5 ч) времени.
а если со скростью 5 км/ч , то затратит х - 0.1 (6 мин. = 0,1 ч.) времени. расстояние одинакоквое:
4(х + 0.5) = 5(х - 0,1)
4x + 2 = 5x - 0,5
x = 2,5 часов
4(2,5+0,5) = 4 * 3 = 12 км весь путь
ответ: 12 км
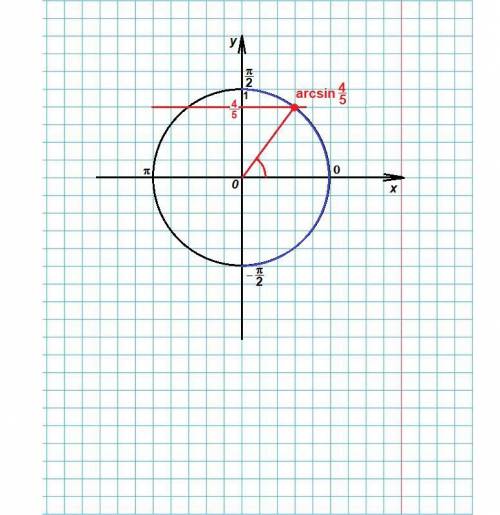
По определению, arcsin 4/5 - это угол α, синус которого равен 4/5.
Причем, это угол, принадлежащий интервалу [- π/2; π/2].
Т.е.
arcsin 4/5 = α, sinα = 4/5, α ∈ [- π/2; π/2].
Построим этот угол на тригонометрической окружности.
Так как синус угла α - это ордината (координата у) точки, повернутой на угол α, то значение синуса 4/5 отмечаем на оси Оу.
Радиус окружности равен 1, поэтому делим его на 5 частей и отмечаем 4 из них.
Через полученную на оси Оу точку проводим горизонтальную прямую. Точка пересечения этой прямой с правой полуокружностью (с синей) и есть точка, соответствующая углу поворота α = arcsin 4/5.
Уравнение :
(Х/ 4 км/ч) – (Х/5 км/ч) = 0,6 часа
Х = 12 км
Для проверки:
со скростью 4 км.ч ему идти 180 минут,
со скоростью 5 км/ч ему идти 144 минуты ,
разница 36 минут.
ответ : Турист должен пройти 12 км.
или:
Обозначим за t - время до отхода поезда (мин) ,
S - расстояние до станции (м).
V1 = 4 км/ч = 4000/60 м/мин - скорость в первом случае
V2 = 5 км/ч = 5000/60 м/мин - скорость во втором случае
Выразим S для обоих случаев
S = (t+30)V1 = (t-6)V2
Из этого равенства выразимt
V1*t + 30*V1 = t*V2 - 6*V2
t = (30* V1+6*V2) / (V2 - V1) = 150 мин
Тогда S = (t + 30) * V1 = 180 * 4000 / 60 = 12000 м = 12 км
ответ: 12 км