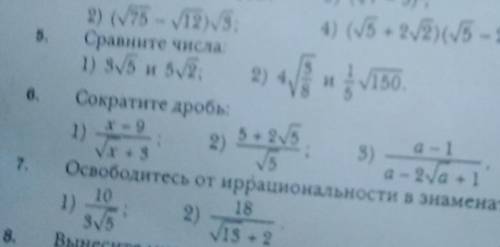
Объяснение:
Средняя линия: EF = 5,5√5 ед.
Площадь трапеции: Sabcd = 82,5 ед²
Объяснение:
Найдем длины (модули) отрезков:
|АВ| = √((Xb-Xa)²+(Yb-Ya)²) = √((-1-(-9))²+(5-1)²) = √80 = 4√5 ед.
|BC| = √((Xc-Xb)²+(Yc-Yb)²) = √((8-(-1))²+(2-5)²) = √90 = 3√10 ед.
|CD| = √((Xd-Xc)²+(Yd-Yc)²) = √((-6-8))²+(-5-2)²) = √245 = 7√5 ед.
|АD| = √((Xd-Xa)²+(Yd-Ya)²) = √((-6-(-9))²+(-5-1)²) = √45 = 3√5 ед.
Два вектора коллинеарны (параллельны), если отношения их координат равны. В нашем случае это векторы
АВ{8;4} и CD{14;7}, так как 8/14 = 4/7. Следовательно, основания трапеции - это отрезки АВ и CD. Меньшая из боковых сторон - AD - высота прямоугольной трапеции.
Тогда имея длины всех сторон и определив, какие из них являются основаниями, найдем:
Среднюю линию: EF = (AB+CD)/2 = 11√5/2 = 5,5√5 ед.
Площадь трапеции: Sabcd = EF·AD = (5,5√5)·3√5 = 82,5 ед²
Или так:
Средняя линия трапеции - отрезок, соединяющий середины боковых сторон. Найдем координаты середин сторон АD и BC - точек E и F соответственно:
Е((Xa+Xd)/2; (Ya+Yd)/2) или Е((-9-6)/2; (1-5)/2).
F((Xb+Xc)/2; (Yb+Yc)/2) или F((-1+8)/2; (5+2)/2). Итак, имеем точки:
E(-7,5;-2) и F(3,5;3,5). Тогда длина средней линии равна:
|EF| = √((Xf-Xe)²+(Yf-Ye)²) = √((3,5-(-7,5))²+(3,5-(-2))²) = √151,25 ед.
Или EF = √151,25 = 5,5√5 ед.
Площадь трапеции равна средней линии, умноженной на высоту.
Sabcd = EF·AD = 5,5√5·3√5 = 3·27,5 = 82,5 ед².
Чтобы решить систему:
7x - 3y = 13;
x - 2y = 5,
Мы с вами применим метод подстановки. Первым действием из второго уравнения системы выражаем одну переменную через другую (переменную x через y).
Система:
7x - 3y = 13;
x = 5 + 2y;
Подставляем в первое уравнение 7x - 3y = 13 вместо x выражение 5 + 2y из второго и получаем:
x = 5 + 2y;
7(5 + 2y) - 3y = 13;
Ищем значение переменной y:
7 * 5 + 7 * 2y - 3y = 13;
35 + 14y - 3y = 13;
11y = -22;
y = -2.
Система уравнений:
x = 5 + 2 * (-2) = 5 - 4 = 1;
y = -2
ответ: (1; -2) решение системы.
См. Объяснение
Объяснение:
№ 5. Сравните числа:
Правило: вносим сомножитель под знак квадратного корня (для этого возводим это число в квадрат), а затем сравниваем подкоренное выражение.
1) 3√5 и 5√2
3√5 = √9·5 = √45
5√2 = √25 · 2 = √50
Так как √45 < √50,
то 3√5 < 5√2
2) 4√(5/8) и 1/5√150
4√(5/8) = √16 · 5 : 8 = √10
1/5√150 = √1 · 150 : 25 = √6
Так как √10 > √6,
то 4√(5/8) > 1/5√150
№ 6. Сократите дробь:
1) (х-9) / (√х+3)
х-9 - можно представить как разность квадратов двух чисел:
х-9 = (√х+3) · (√х-3), тогда
(√х+3) · (√х-3) /(√х+3) = √х-3
2) (5+2√5)/√5
В числителе вынесем √5 за скобки (чтобы сократилось со знаменателем), тогда получим:
√5 · (√5 +2) /√5 = √5 +2
3) (а-1) / (а-2√а+1)
а-1 можно рассматривать как разность квадратов двух чисел:
а-1 = (√а +1) · (√а -1);
(а-2√а+1) - это квадрат разность двух чисел:
(а-2√а+1) = (√а -1)².
Следовательно:
(а-1) / (а-2√а+1) = (√а +1) · (√а -1) / (√а -1)² = (√а +1)/(√а -1)
№ 7. Освободитесь от иррациональности в знаменателе:
Правило: дробь не изменит своего значения, если её числитель и знаменатель умножить на одно и то же число, не равное нулю.
1) 10 / 3√5
Умножим числитель и знаменатель этой дроби на√5:
10 √5 / 3 · 5 = 2√5/3
2) 18 / (√13+2)
Умножим числитель и знаменатель на (√13-2) - это нам даст в знаменателе разность квадратов двух чисел:
18 · (√13-2) / (√13+2) · (√13-2) = 18 · (√13-2) / (13 -4) = 18 · (√13-2) / 9 =
= 2· (√13-2)