Со скобками нужно решать, смотря какие знаки стоят в примере + или --
Объяснение:
При сложении 2 многочленов, нужно представить их в стандартном виде, потом чтобы сложить их, нужно:
1) Раскрыть скобки, не меняя знаки, потому что при + не меняется знак на противоположный.
При -- нужно опустить скобки и заменить все знаки одночленов внутри скобок на противоположные, например: 3х2-5ху-7х2у+(5ху--3х2+8х2у) =3х2-5ху-7х2у+5ху-3х2+8х2у.
Без скобок решается по разложения многочленов на множители:
1. Вынесение общего множителя за скобки
10а+25b
группировки
сокращённого умножения.
Да и ты можешь посмотреть ролики в интернете, найми репетитора.
1)
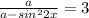

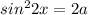
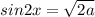
Так как значения синуса не могут быть большими единицы, получаем:

Так как выражение под радикалом и собственно весь радикал не могут быть отрицательными получаем:

Откуда получаем:
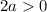

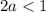
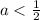
Объединяя полученные результаты получаем: a∈
ответ: a∈
2)

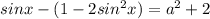


Получаем квадратное уравнение относительно t:

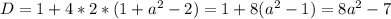


Исходя из того что данное уравнение должно иметь лишь одно решение получаем, что дискриминант должен быть равен нулю:
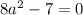
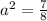
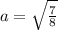
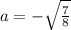
Но так как нам нужно только одно решение в заданном промежутке получаем:

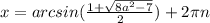

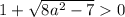
неравенство не имеет решений
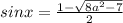


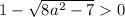

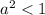
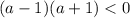
Получаем, что при a∈ данное уравнение имеет лишь один корень
данное уравнение имеет лишь один корень
ответ: a∈
Объяснение: