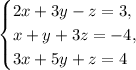
1) Знак неравенства меняется если основное число меньше 1;
2) Если знак неравенства, то точка будет неполная;
3) Если знак неравенства больше равно, меньше равно, то точка будет полная.
4) Полная точка ( зарисованная внутри );
5) Неполная точка ( не зарисованная внутри );
6) Если знак неравенства, то скобка "(" ;
7) Если знак неравенства больше равно, меньше равно, то скобка
"[" ;
8) В какую сторону показывает носик неравенства, в ту сторону рисуем допустимые значения;
9) Не забываем что числа можно подавать как меньшее число в степени;
Теперь когда всё вспомнили можно решать:
1) 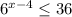
Подаём число 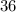 как
как 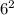
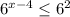
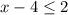
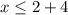
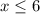
Не забываем что можно сократить основы если они одинаковые.
Теперь рисуем прямую и на ней отмечаем точку которую получили.
Фото прямых прикрепил.
Точка полная так как имеем 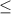 .
.
Допустимые значения направленные в левую сторону так как "носик" знака неравенства направлен именно туда.
x ∈ ( -∞, 6 ]
2) 
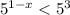
Подаём число 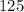 как
как 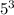
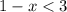
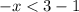
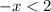
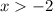
Сменили знак неравенства, так как перенесли - в другую часть неравенства.
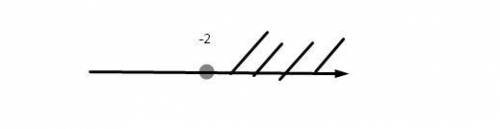
Теперь рисуем прямую и на ней отмечаем точку которую получили.
Точка неполная, так как имеем > .
x ∈ ( -2, +∞ )
3) 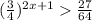
Подаём 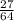 как
как 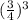 .
.
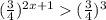
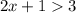
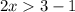
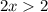
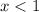
Сменили знак неравенства, так как 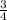 меньше 1.
меньше 1.
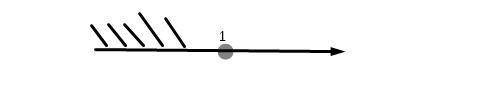
Теперь рисуем прямую и на ней отмечаем точку которую получили.
Точка неполная, так как имеем  .
.
x ∈ ( -∞, 1 )

Пусть за х дней может закончить Катя, тогда еѐ производительность равна / х .
А за у дней может закончить Алиса, тогда еѐ производительность равна / у .
Т.к. они могут напечатать курсовую работу за 6 дней,
то /х + /у = 1/
Если сначала % = / части курсовой напечатает Катя,
а затем завершит работу Алиса, то Алисе остается
% = / части курсовой.
Вся курсовая работа будет выполнена за 12 дней т.е.
( /) х + (/ ) у = .
Решим систему:
/х + /у = / ,
(/) х + (/ ) у = .
+ = ,
+ = ;
у = − , ;
+ * ( − , ) = *( − , )
у = − , ;
, ² − + = ;
у = − , ;
² − + = ;
² − + = ;
= , у =
или = , у = . - не подходит, т.к. Катя печатает быстрее, чем Алиса.
Значит, Катя может напечатать курсовую работу за 10 дней.
ответ. за 10 дней
x = -5
y = 4
z = -1
Объяснение:
Первую строку умножим на 3 и прибавим ко второй:
(6x + 9y - 3z) + (x + y + 3z) = 9 + (-4)
7x + 10y = 5
Получается:
Первую строку прибавим к третьей:
(2x + 3y - z) + (3x + 5y + z) = 3 + 4
5x + 8y = 7
Получается:
Теперь, вторую строку умножим на 8, а третью - на 10 и вычтем из второй третью:
(56x + 80y) - (50x + 80y) = 40 - 70
6x = -30
Получаем такую систему:
Находим x:
6x = -30
x = -5
Теперь ищем y по второй строке:
7 * (-5) + 10y = 5
-35 + 10y = 5
10y = 40
y = 4
Теперь z, по первой:
2 * (-5) + 3 * 4 - z = 3
-10 + 12 - z = 3
2 - z = 3
z = -1