(-3,6-1,6-4,8): (-2)= -10 * (-1/2) = 5
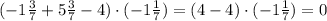
Первая производная
f'(x) = 4·(x-5)^3·(x+2)^3+3·(x-5)^2·(x+2)^4
или
f'(x)=7·(x-5)^2·(x-2)·(x+2)^3
Находим нули функции. Для этого приравниваем производную к нулю
(x-5)^2·(x-2)·(x+2)^3 = 0
Откуда
x1 = 5
x2 = -2
x3 = 2
(-∞ ;-2),f'(x) > 0-функция возрастает
(-2; 2),f'(x) < 0-функция убывает
(2; 5),f'(x) > 0-функция возрастает
(5; +∞),f'(x) > 0-функция возрастает
В окрестности точки x = -2 производная функции меняет знак с (+) на (-). Следовательно, точка x = -2 - точка максимума. В окрестности точки x = 2 производная функции меняет знак с (-) на (+). Следовательно, точка x = 2 - точка минимума.
a) (-3.6-1.6-4.8):(-2)= -10:(-2)=5
b) (-1³/₇ + 5³/₇-4)·(-1¹/₇)= (-¹⁰/₇+³⁸/7-4)·(-1¹/₇)=(²⁸/₇-4)·(-1¹/₇)=(4-4)·(-1¹/₇)=0
ответ:0