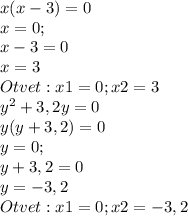
Тұмсықта бойлай созылған қырлар мен қатпарлар болады, тілі - ұзын және нығыз, тұмсықтың ұзындығындай алға созылып шығуға бейім, тілінің ұшы үшкір, арнайы сөл шығатындықтан, жабысқақ болып келеді. Тоқылдақтар осы тұмсықтың жәрдемімен қабық тесігі мен жарығына және сүрегіне тереңірек бойлап, бунақденелілерді және олардың дернәсілдерін жапсырып немесе шаншып алады. Жабын қауырсындары - қатқыл, көбінесе ашық түсті. Құйрығы - ұзын, конус пішінді қатқыл. Құс құйрығын таяныш етіп, қысқа және өте имек, өткір тырнақтарымен тік бетке жабысады. Аяқтары - қысқа және күшті екі саусағы - алға, екі саусағы - артқа бағытталған 4 саусағы болады. Орман құсы, отырықшы өмір сүреді, кейде шағын қашықтыққа қоныс аударады. Топ та үйір де түзбейді. Моногамиялы, жұбын көптеген жылдар бойы жиі сақтайды. Қабықта және сүректе тіршілік ететін бунақденелілерді және солардың дернәсілдерін жейді, дегенмен затия бетіндегі азықтарды да шоқиды. Күзде және қыста тұқымдар мен жемістерді жейді. Тоқылдақтар отрядында 207 түрді қамтитын 34-35 туыс бар. Қазақстанда 5 туыстан 8 түр кездеседі.
Орман шаруашылығында тоқылдақтардың пайдасы үлкен. Олар күн сайын бірнеше жүз зиянды насекомдарды қырады. Тоқылдақтар әсіресе жаз айларында пайдалы, өйткені, олар бұл кезде насекомдармен қоректенеді. Қыста тоқылдақтар көпшілігінде кылқанды ағаштардың дәндерімен қоректенеді. Үзіп алған жаңғақтарын өздері шоқып жасаған ағаш қуыстарына бекітіп қойып, оны қаты тұмсығымен жарып, ішінен дәнін алып жейді. Пайдаланылып болған бүршік қабығын жерге түсіреді. Тоқылдақтардың жаңғақтарды апарып бекітіп қойып, ішінен дәнін алып жейтін жерін “дүкен” деп атайды. Мұндай “дүкендердің” астында қарағайдын, бірнеше мыңдаған тұқымы алынған бүрлері үйіліп қалады. Тоқылдақтардың келтіретін аздаған осындай зияндарынан, олардың пайдасы аздаған көп. Сондықтан да халык “тоқылдақ — тоғай дәрігері” деп атайды[1].
Дереккөздер
Пример 1. Почему квадрат корня квадратного из неотрицательного числа равен самому этому числу? Другими словами, почему
(√a)² = a?
ответ. По определению квадратного корня.
Пример 2. Почему
ответ. По определению логарифма.
Вспомните определение квадратного корня: квадратным корнем из неотрицательного числа а (а ≥ 0) называют неотрицательное число √a , квадрат которого равен а.
А теперь повторите определение логарифма: логарифмом положительного числа N (N > 0) по положительному и не равному единице основанию а (а > 0, а ≠ 1) называют такое число loga N, что основание а в степени loga N равно N. Мы убедились в том, что обе формулы (из примеров 1 и 2) представляют собой не что иное, как формальную запись определений квадратного корня и логарифма, соответственно.
Пример 3. Почему две параллельные прямые лежат в одной плоскости?
ответ. По определению параллельных прямых.
Пример 4. Почему сумма внутренних углов треугольника равна 180°?
ответ. По теореме о сумме углов треугольника.
Пример 5. Почему сумма всех нечетных чисел, начиная с 1 до 2n + 1, равна квадрату натурального числа n?
Отвечая на этот вопрос, мы не можем сослаться на одну из теорем курса. Поэтому нужно приступить к доказательству. Вы найдете его в главе, посвященной математической индукции.
Задачи
Глава 1 Геометрические задачи на плоскости
Обозначения: а, b, с — стороны треугольника; А, В, С — углы, лежащие против этих сторон, соответственно; mа — медиана стороны а; lA — биссектриса угла А; ha — высота, опущенная на сторону а; R — радиус описанной окружности; r — радиус вписанной окружности; P = 2р — периметр многоугольника.
Длиной биссектрисы внешнего угла А треугольника называется отрезок биссектрисы, заключенный между точкой А и точкой пересечения биссектрисы с продолжением стороны а.
Отношение площадей двух треугольников, имеющих общий угол, равно отношению произведений сторон, заключающих этот общий угол.
Имеет место формула, выражающая длину медианы треугольника через длины его сторон:.
Если в многоугольник можно вписать окружность, то его площадь S = pr.
Площадь четырехугольника: S = ½ d1d2 sin α, где d1 и d2 — длины его диагоналей, а α — угол между ними.
При решении планиметрических задач приходится применять производные пропорции.
Если .
Если , то
, где комбинация знаков берется любая, но одинаковая для числителя и знаменателя.
1.1. Вокруг правильного треугольника ABC описана окружность O радиусом R. Окружность O1 касается двух сторон AB и BC треугольника и окружности O. Найдите расстояние от центра окружности О1 до вершины А.
1.2. Высота равнобедренного треугольника с углом α при основании больше радиуса вписанного в него круга на m. Определите основание треугольника и радиус описанной окружности.
1.3. Докажите, что радиус окружности, делящей пополам стороны треугольника, вдвое меньше радиуса окружности, описанной около этого треугольника.
1.4. В треугольнике соединены основания биссектрис. Найдите отношение площади данного треугольника к площади образовавшегося треугольника, если стороны данного треугольника относятся как p : q : l.
1.5. Даны углы A, B, C треугольника ABC. Пусть окружность касается сторон BC, AC и AB треугольника соответственно в точках A1, B1, C1. Найдите отношение площади треугольника A1B1C1 к площади треугольника ABC.
1.6. Дан треугольник ABC, углы B и C которого относятся как 3 : 1, а биссектриса угла А делит площадь треугольника в отношении 2 : 1. Найдите углы треугольника.
1.7. Найдите длину l биссектрисы внешнего угла А треугольника, если даны его стороны b и c и угол А между ними (b ≠ c).
1.8. В треугольнике площади S, с острым углом α при вершине А биссектриса угла А в p раз меньше радиуса описанного и в q раз больше радиуса вписанного круга. Найдите сторону треугольника, лежащую против угла А.
1.9. В треугольнике ABC проведены биссектрисы AM и BN. Пусть O — точка их пересечения. Известно, что
AO : OM = √3 : 1, а BO : ON = 1 : (√3 − 1).
Найдите углы треугольника.
1.10. Внутри угла а взята точка M. Ее проекции P и Q на стороны угла удалены от вершины O угла на расстояния OP = p и OQ = q. Найдите расстояния MP и MQ от точки M до сторон угла.
1.11. В остроугольном треугольнике две высоты равны 3 и 2√2 см, а их точка пересечения делит третью высоту в отношении 5 : 1, считая от вершины треугольника. Найдите площадь треугольника.
1.12. В треугольнике ABC разность углов B и C равна π/2. Определите угол C, если известно, что сумма сторон b и c равна k, а высота, опущенная из вершины A, равна h.
1.13. В треугольнике ABC имеется точка O, такая, что углы ABO, ВСО и CAO равны α. Выразите ctg α через площадь треугольника и его стороны.
1.14. В треугольнике ABC дана разность φ углов A и В (φ = A − В > 0). Известно, что высота, опущенная из С на AB, равна BC − AC. Найдите углы треугольника.
Объяснение:
решение смотри на фотографии