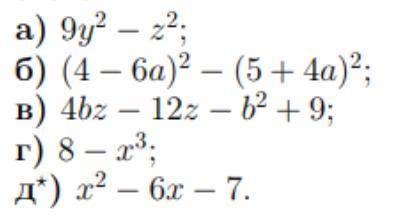
а). =(3y-z)(3y+z)
б). =(4-6a-(5+4a))(4-6a+(5+4a))=(4-6a-5-4a)(4-6a+5+4a)=(-1-10a)(9-2a)
в). =4z(b-3)-(b^2-9)=4z(b-3)-(b-3)(b+3)=(b-3)(4z-(b+3))=(b-3)(4z-b-3)
г). 2^3-х^3=(2-х)(2^2+2х+х^2)=(2-х)(4+2х+х^2)
д). =х^2+х-7х-7=х(х+1)-7(х+1)=(х+1)(х-7)
1. Сначала надо спростить левую часть уравнения — используем формулу сокращённого умножения ( а - в )( а + в ) = а² - в² :
( 5х + 2 ) - ( 25х² - 9 ) = 73
2. Потом открываем скобки, поскольку перед 2- ми стоит минус, то знаки меняются на противоположные :
5х + 2 - 25х² + 9 = 73
3. Сводим подобные слогаемые и переносимости всё в левую часть:
- 25х² + 5х + 11 - 73 = 0
- 25х² + 5х - 62 = 0
4. Умножим обе части уравнения на -1:
- 25х² + 5х - 62 = 0 | × (-1)
25х² - 5х + 62 = 0
5. Получилось квадратное уравнение, решаем через дискриминант:
D = (-5)² - 4 × 25 × 62 = 25 - 6200 = -6175
6. Поскольку -6175 < 0, D < 0, тогда уравнение не имеет корней.
ответ : корней нет
Задания на свойства и графики квадратичной функции вызывают, как показывает практика, серьезные затруднения. Это довольно странно, ибо квадратичную функцию проходят в 8 классе, а потом всю первую четверть 9-го класса "вымучивают" свойства параболы и строят ее графики для различных параметров.
Это связано с тем, что заставляя учащихся строить параболы, практически не уделяют времени на "чтение" графиков, то есть не практикуют осмысление информации, полученной с картинки. Видимо, предполагается, что, построив десятка два графиков, сообразительный школьник сам обнаружит и сформулирует связь коэффициентов в формуле и внешний вид графика. На практике так не получается. Для подобного обобщения необходим серьезный опыт математических мини исследований, которым большинство девятиклассников, конечно, не обладает. А между тем, в ГИА предлагают именно по графику определить знаки коэффициентов.
Не будем требовать от школьников невозможного и предложим один из алгоритмов решения подобных задач.
Итак, функция вида y = ax2 + bx + c называется квадратичной, графиком ее является парабола. Как следует из названия, главным слагаемым является ax2. То есть а не должно равняться нулю, остальные коэффициенты (b и с) нулю равняться могут.
Посмотрим, как влияют на внешний вид параболы знаки ее коэффициентов.
Самая зависимость для коэффициента а. Большинство школьников уверенно отвечает: " если а > 0, то ветви параболы направлены вверх, а если а < 0, – то вниз". Совершенно верно. Ниже приведен график квадратичной функции, у которой а > 0.
y = 0,5x2 - 3x + 1
В данном случае а = 0,5

А теперь для а < 0:
решение смотри на фотографии