5.На тарелке лежат одинаковые на вид пирожки: 3 с мясом, 3 с капустой и 4 с вишней. Саша наугад берёт один пирожок. Найдите вероятность того,
что пирожок окажется с вишней.
6.На тарелке лежат одинаковые на вид пирожки: 2 с творогом, 13 с рисом и
5 с яблоками. Лёша наугад берёт один пирожок. Найдите вероятность того,
что пирожок окажется с яблоками.
7.В фирме такси в данный момент свободно 20 машин: 3 чёрные, 3 жёлтые
и 14 зелёных. По вызову выехала одна из машин, случайно оказавшаяся
ближе всего к заказчику. Найдите вероятность того, что к нему приедет
жёлтое такси.
8.В фирме такси в данный момент свободно 15 машин: 3 чёрные, 6 жёлтых
и 6 зелёных. По вызову выехала одна из машин, случайно оказавшаяся
ближе всего к заказчику. Найдите вероятность того, что к нему приедет
жёлтое такси.
9.В фирме такси в данный момент свободно 30 машин: 6 чёрных, 3 жёлтых
и 21 зелёная. По вызову выехала одна из машин, случайно оказавшаяся
ближе всего к заказчику. Найдите вероятность того, что к нему приедет
жёлтое такси.
10. В фирме такси в данный момент свободно 12 машин: 3 чёрных, 3 жёлтых и 6 зелёных. По вызову выехала одна из машин, случайно оказавшаяся
ближе всего к заказчику. Найдите вероятность того, что к нему приедет
жёлтое такси.
11. В фирме такси в данный момент свободно 10 машин: 5 чёрных, 2 жёлтых и 3 зелёных. По вызову выехала одна из машин, случайно оказавшаяся
ближе всего к заказчику. Найдите вероятность того, что к нему приедет
жёлтое такси.
За ранее !
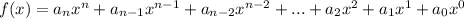 ,
, 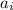 - коэффициент
- коэффициент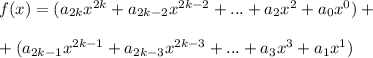
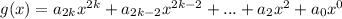
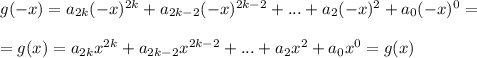
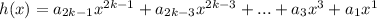

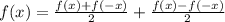


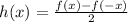

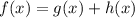 , где g(x) - чётная, а h(x) - нечётная функция.
, где g(x) - чётная, а h(x) - нечётная функция.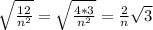
Это просто. Формула вероятности: P= m/n, где m - благоприятные события, n- все возможные. И все шуруй.
К примеру, в 5 задании:
1)Сначало узнаем сколько всего пирожков в тарелке.
4 + 3 + 3 = 10
2.)Поделим количество всех пирожков на количество пирожков с вишней.(Благоприятные)
4 / 10 = 0.4 – вероятность
Или к примеру 9 задание. Кол-во свободных авто 30, отсюда нам нужно жёлтое авто, значит 3/30=10