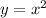В прямоугольном треугольнике проведена высота к гипотенузе. Какие углы эта высота образует с катетами, если больший из острых углов этого треугольника равен 50°?

1. Угол с меньшим катетом равен

°.

2. Угол с большим катетом равен

!

👇

Ответ:

mashaguglik

21.08.2022

ΔАВС , ∠С=90° , ∠В=50° ⇒ ∠А=90°-∠В=90°-50°=40°

СН ⊥ АВ ⇒ ∠СНА=90° и ∠СРВ=90° .

Рассм. ΔВСН . Он прямоугольный и ∠В=50° , тогда ∠ВСН=90°-50°=40°. Это угол, образованный высотой СН с меньшим катетом (катет ВС лежит против меньшего острого угла ΔАВС).

Рассм. ΔАСН . Он прямоугольный и ∠А=40° , тогда ∠АСН=90°-40°=50°. Это угол, образованный высотой СН с бОльшим катетом АС (катет АС лежит против бОльшего острого угла ΔАВС).

Замечание. Так как у треугольников ΔАВС , ΔВСН и ΔАСН все три угла равны, то эти треугольники подобны .

В прямоугольном треугольнике проведена высота к гипотенузе. Какие углы эта высота образует с катетам

4,8(78 оценок)

Открыть все ответы

Ответ:

Shkolnik228007

21.08.2022

Ну алгоритм не алгоритм, а принцип построения поясню.
Во первых слева дополнительное слагаемое +1 "сдвигает" график исходной функции y=x^2

на одну единицу вверх вдоль (параллелно) оси OY. График "поднимается" .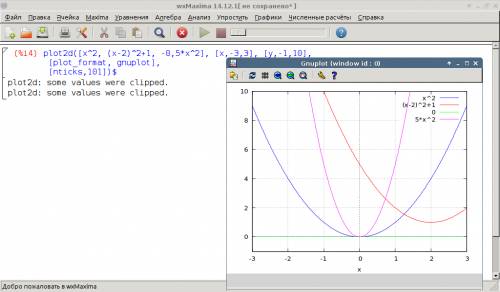
(Если бы было -1, график исходной функции сдвинулся бы на 1 вниз).

Вообще,чтобы получить график функции f(x)+B, исходный график нужно сместить на B единиц вверх (при B>0), или вниз ( при B<0).

Далее
График функции y=f(x+C) получается из исходного графика функции y=f(x) путем сдвига его вправо (С<0) или влево (C>0) на C единиц.

Т.е. в нашем случае нам нужно сдвинуть исходный график y=x^2 на 1 единицу вверх и на 2 единицы вправо.
Ну и коэффициент a при х^2 "растягивает" или "сжимает" график к вертикальной оси.
Может даже "Зеркально отразить" исходный график (при a=-1).

Чтобы из исходного графика y=x^2 получить график y=a*x^2
нужно координаты всех его точек (на практике только нескольких опорных пересчитать по следующему принципу
(x, a*x^2). Т.е координата X, выбранной точки не меняется, а координату Y надо умножить на a.

P.S. В свое время в учебниках что-то подобное писали, недавно я встречал подобные и более подробные рассуждения в книге:
Зельдович Я. Б. "Высшая математика для начинающих и ее приложения к физике"

Построить графики функций (3 модели) и сформулируйте алгоритм построения графика функции y=a(x+t)^2+

Построить графики функций (3 модели) и сформулируйте алгоритм построения графика функции y=a(x+t)^2+

4,6(42 оценок)

Ответ:

Molly11111

21.08.2022

Объяснение:

1) Коэффициент при старшей степени (x^2) положительный, соответственно, ветви параболы направлены вверх

2) Чтобы уравнение имело 2 различных корня, дискриминант должен быть больше 0 (если дискриминант равен 0, то ответом являются 2 одинаковых корня; если дискриминант меньше 0, то корней на множестве действительных чисел нет)

D=b^2-4ac=(a-5)^2-4*1*9=a^2-10a+25-36=a^2-10a-11

a^2-10a-11>0

Найдем нули:

a^2-10a-11=0

a1=-1

a2=11

3) Выражение можно разложить на множители по формуле a(x-x1)(x-x2)

1*(a+1)(a-11)

(a+1)(a-11)>0

Расставим на числовой оси эти точки (выколотые) и знаки, получим ответ

a∈(-∝;-1)U(11;+∝)

ответ: a∈(-∝;-1)U(11;+∝)