ответ: при х=1 и при х=-1
Объяснение:Точки пересечения графиков данных функций y=x²+4x+1 и y=kx можно найти, приравняв значения функций:
x²+4x+1 = kx
x²+4x+1 - kx =0
x²+(4-k)·x+1 = 0
По условию прямая y=kx и парабола y=x²+4x+1 имеют только одну общую точку, значит дискриминат полученного квадратного уравнения равен 0 (чтобы квадратное уравнение имело единственный корень), ⇒D=(4-k)² - 4·1·1= 16-8k+k²-4= k²-8k+12
k²-8k+12=0
k₁=2, k₂=6
Поэтому прямая у=2х и парабола y=x²+4x+1 имеют только одну общую точку⇒x²+4x+1 =2х⇒x²+2x+1 =0⇒ (х+1)²=0 ⇒ х=-1
прямая у=6х и парабола y=x²+4x+1 имеют только одну общую точку⇒x²+4x+1 =6х⇒ x²-2x+1 =0⇒ (х-1)² =0 ⇒ х=-1
а) 17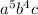 г) -7
г) -7
Объяснение:
Одночлен — произведение, состоящее из числового множителя и одной или нескольких переменных, взятых каждая в неотрицательной степени.
Неотрицательные числа - это все положительные числа и 0.
а) 17 - числовой множитель, умноженный на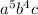 - несколько переменных, каждая из которых в неотрицательной степени: ПОДХОДИТ
- несколько переменных, каждая из которых в неотрицательной степени: ПОДХОДИТ
б) здесь сумма одночленов: НЕ ПОДХОДИТ
в) -23 - числовой множитель, умноженный на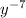 - переменная, взятая в отрицательной степени: НЕ ПОДХОДИТ
- переменная, взятая в отрицательной степени: НЕ ПОДХОДИТ
г) -7 - числовой множитель, умноженный на переменную в степени 0: ПОДХОДИТ