
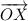 , точку О будем считать началом координат. Т.е. мы получили ось ОХ, которая разбивает всю плоскость на верхнюю и нижнюю полуплоскости. Если в каждой полуплоскости лежит по 299 точек, то это и есть средняя линия. Если в верхней полуплоскости n точек, а в нижней m и, допустим, m<n, то повернем прямую ОХ вокруг точки О против часовой стрелки до тех пор, пока она первый раз не пройдет через другую точку ( допустим Y). В результате такого поворота, количество точек в каждой полуплоскости либо останется неизменным, либо уменьшится на 1, либо увеличится на 1. Это так, потому что никакие 3 точки не лежат на одной прямой. Причем, если в одной полуплоскости число точек увеличилось на 1, то во второй - уменьшилось на 1, т.к. общее количество точек 598 (не считая тех двух, через которые проходит прямая) остается неизменным. Это значит, что после такого поворота разность между количеством точек в верхней и нижней полуплоскости либо не изменилась, либо уменьшилась/увеличилась на 2.
, точку О будем считать началом координат. Т.е. мы получили ось ОХ, которая разбивает всю плоскость на верхнюю и нижнюю полуплоскости. Если в каждой полуплоскости лежит по 299 точек, то это и есть средняя линия. Если в верхней полуплоскости n точек, а в нижней m и, допустим, m<n, то повернем прямую ОХ вокруг точки О против часовой стрелки до тех пор, пока она первый раз не пройдет через другую точку ( допустим Y). В результате такого поворота, количество точек в каждой полуплоскости либо останется неизменным, либо уменьшится на 1, либо увеличится на 1. Это так, потому что никакие 3 точки не лежат на одной прямой. Причем, если в одной полуплоскости число точек увеличилось на 1, то во второй - уменьшилось на 1, т.к. общее количество точек 598 (не считая тех двух, через которые проходит прямая) остается неизменным. Это значит, что после такого поворота разность между количеством точек в верхней и нижней полуплоскости либо не изменилась, либо уменьшилась/увеличилась на 2.
{4x > 0
1) 4x²+5x-6 > 0
D = 25+96 = 121
x₁,₂ = (-5⁺₋11)/8 = 0,75; -2
+ - +
₀₀>x
-2 0,75
2) 7x > 0
x > 0
₀> x
0
3)
-2 0,75
₀₀₀> x
0
x∈(0,75; ∞)
2. {х²-16 < 0
{2x ≥ 18
1) x²-16 < 0
(x-4)(x+4) < 0
x₁ = 4; x₂ = -4
+ - +
₀₀> x
-44
2) 2x ≥ 18
x ≥ 9
.>x
9
3)
-44
₀₀.>x
9
Система решений не имеет