ответ: 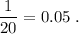
Нам благоприятствуют 45 чисел. Возьмем любую цифру и начнем в ней строить всевозможные подходящие числа. Для каждого из чисел от 3 до 7 включительно есть по 2*3=6 пар (два числа и три их расположения). Для цифр 1, 8, 9 есть по три числа (131, 311, 113 и т. д.). Для цифры 0 - одно (200), а для 2 - пять чисел (220, 202, 224, 242, 422). Итого:
5 * 6 + 3 * 3 + 1 + 5 = 45 (чисел).
А всего трехзначных чисел:
9 * 10 * 10 = 999 - 100 + 1 = 900.
Тогда искомая вероятность равна:
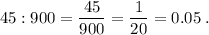
Примечание:
Вот эти 45 чисел:
113, 131, 311, 220, 202, 224, 242, 422, 331, 313, 133, 335, 353, 533, 442, 424, 244, 446, 464, 644, 553, 535, 355, 557, 575, 755, 664, 646, 466, 668, 686, 866, 775, 757, 577, 779, 797, 977, 886, 868, 688, 997, 979, 799, 200.
Если обозначить через x1, y1 и z1 координаты точки А, а через x2, y2 и z2 - координаты точки В, то искомое уравнение плоскости можно записать в виде определителя:
x-x1 y-y1 z-z1
x2-x1 y2-y1 z2-z1 = 0.
A B C
Здесь А=3, В=-4, С=-1 - координаты нормального вектора плоскости 3x-4y-z+5=0.
Подставляя в определитель координаты точек, получаем определитель:
x-8 y-7 z+1
-3 -8 4 = 0
3 -4 -1
Раскрывая этот определитель по первой строке, получаем уравнение плоскости 24x+9y+36z-219=0. Подставляя в него координаты точек А и В, убеждаемся, что эти точки принадлежат плоскости. Кроме того, нормальный вектор данной плоскости, имеющий координаты (24;9;36), перпендикулярен нормальному вектору плоскости 3x-4y-z+5=0, так как их скалярное произведение равно нулю: 24*3+9*(-4)+36*(-1)=0.
ответ: 24x+9y+36z-219=0
25х - 25 меньше или равно 30х - 36
25х -30 х меньше или равно 25 - 36
-5х меньше или равно -11 /*(-1)
5х больше или равно 11
х больше или равен 2.2
3)3х-2<3(x+2)-5
3х - 2 < 3х + 6 - 5
3х-3х < 2 + 6 - 5
х < 3
4) 2х-3>0
5-x>0
2х > 3
4x > 0
x > 1.5
x > 0