Question

Y=0,25x^2-2x+1 можно ли построить функцию если дискриминант с корнем? и вообще могу построить параболу без дискриминанта?

Answer 1

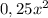y=$0,25x^{2}$-2x+1

1. Ветви параболы, являющейся графиком данной функции, направлены вверх, т. к. а=0,25>0

2. Найдем координаты вершины параболы:

х=$\frac{-b}{2a}=\frac{2}{0,5}=4$ 

y=0,25*16-8+1=-3

Значит вершина параболы (4; -3)

3. Точки пересечения с осью ох:

0,25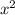$x^{2}$-2x+1=0

$x^{2}$ -8x+4=0

D=64-16=48

x1=4-2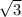$\sqrt{3}$ ,  x2=4+2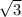$\sqrt{3}$

4. Точки пересечения с осью оу:

у=1

Далее построить параболу по вершине и найденным точкам (там, где получилось с корнями, взять приближенные значения)