Как-то кривенько все получается, либо приблизительно, либо с корнями...
Ну смотрите сами.
1. А+В = 5
А*В = -2
Выражаем А через В
А = (5-В) и подставляем во второе выражение
(5-В)* В = -2, раскрываем скобки и получаем кв. уравнение
В в кв - 5В - 2= 0, по формуле находим корни В1 В2
В1 = ( 5- кв корень(25+8)):2 = 2.5 - кв корень(33)/2
В2 = ( 5 + кв корень(25+8))/2 = 2.5 + кв корень(33)/2
Потом находим А1 и А2
А1 = 5 - (2.5 - кв корень(33)/2) = 2.5 + кв корень (33)/2
А2 = 5 - (2.5 + кв корень(33)/ 2) = 2,5 - кв корень(33)/2
Теперь ищем (А-В) в кв (А1-В1) и (А2-В2)
1. ((2.5+кв к(33)/2)-(2.5-кв.к(33)/2)в кв =( кв к(33))в кв = 33
2. ((2.5-кв к(33)/2)- (2,5+кв к(33)/2)в кв = (-кв к(33))в кв = 33
Проверьте, может где-то перемудрила, но основная мысль такова.
Удачи!
1.
a)
x² + 4x + 10 ≥ 0
Рассмотрим функцию у = x² + 4x + 10.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² + 4x + 10 = 0
D = 16 - 40 = - 24 < 0
нулей нет, значит график не пересекает ось Ох.
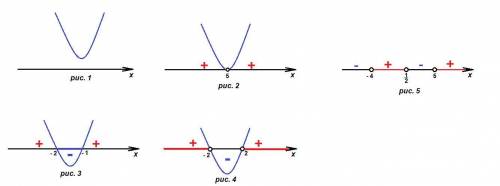
Схематически график изображен на рис. 1.
у > 0 при x ∈ (- ∞; + ∞)
ответ: 2) Решением неравенства является вся числовая прямая.
b)
- x² + 10x - 25 > 0 | · (- 1)
x² - 10x + 25 < 0
Рассмотрим функцию у = x² - 10x + 25.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² - 10x + 25 = 0
(x - 5)² = 0
x = 5
Схематически график изображен на рис. 2.
у < 0 при x ∈ {∅}
ответ: 1) Неравенство не имеет решений.
c)
x² + 3x + 2 ≤ 0
Рассмотрим функцию у = x² + 3x + 2.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² + 3x + 2 = 0
D = 9 - 8 = 1
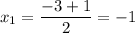
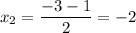
Схематически график изображен на рис. 3.
у ≤ 0 при x ∈ [- 2; - 1]
ответ: 4) Решением неравенства является закрытый промежуток.
d)
- x² + 4 < 0 | · (- 1)
x² - 4 > 0
Рассмотрим функцию у = x² - 4.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² - 4 = 0
x² = 4
x = ± 2
Схематически график изображен на рис. 4.
у > 0 при x ∈ (- ∞; - 2) ∪ (2; + ∞)
ответ: 6) Решением неравенства является объединение двух промежутков.
___________________________
2.
(x - a)(2x - 1)(x + b) > 0
x ∈(- 4; 1/2) ∪ (5; + ∞)
Решение неравенства показано на рис. 5.
Найдем нули функции у = (x - a)(2x - 1)(x + b).
(x - a)(2x - 1)(x + b) = 0
(x - a) = 0 или (2x - 1) = 0 или (x + b) = 0
x = a x = 1/2 x = - b
Из решения неравенства следует, что нулями являются числа - 4, 1/2 и 5. Значит
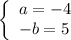 или
или 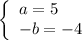
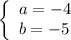 или
или 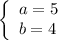
ответ: a = - 4, b = - 5 или a = 5, b = 4.
чтобы закреплять, добавлять или удалять фрагменты, используйте значок редактирования.чтобы закрепить фрагмент, нажмите на него и удерживайте. незакрепленные объекты будут удалены через час.чтобы закреплять, добавлять или удалять фрагменты, используйте значок редактирования.чтобы закрепить фрагмент, нажмите на него и удерживайте. незакрепленные объекты будут удалены через час.чтобы закреплять, добавлять или удалять фрагменты, используйте значок редактирования.чтобы закрепить фрагмент, нажмите на него и удерживайте. незакрепленные объекты будут удалены через час.чтобы закреплять, добавлять или удалять фрагменты, используйте значок редактирования.чтобы закрепить фрагмент, нажмите на него и удерживайте. незакрепленные объекты будут удалены через час.чтобы закрепить фрагмент, нажмите на него и удерживайте. незакрепленные объекты будут удалены через час.чтобы закреплять, добавлять или удалять фрагменты, используйте значок редактирования.чтобы закрепить фрагмент, нажмите на него и удерживайте. незакрепленные объекты будут удалены через час.чтобы закреплять, добавлять или удалять фрагменты, используйте значок редактирования.чтобы закрепить фрагмент, нажмите на него и удерживайте. незакрепленные объекты будут удалены через час.чтобы закреплять, добавлять или удалять фрагменты, используйте значок редактирования.чтобы закрепить фрагмент, нажмите на него и удерживайте. незакрепленные объекты будут удалены через час.чтобы закреплять, добавлять или удалять и
там есть проверка, так что, все будет под корнем)