x^2 + px + 7 = 0 x_2 - x_1 = 2V2, x_2 > 0, x_1 > 0, p ?
{x_1 + x_2 = -p > p = -x_1 - x_2
{x_2 - x_1 = 2V2 x_2 = x_1 + 2V2 подставим в 3--е уравнение.
{x_1 *x_2 = 7 > x_1 * (x_1 + 2v2) = 7 Пусть х_1 = z
z^2 + 2V2z - 7 = 0
D = b^2 - 4ac = 8 + 28 = 36 = 6^2 > 0
z_1 = x_1 = (-b + VD) / 2a = ( -2V2 + 6) / 2 = 3 - V2 > 0 подходит по условию.
z_2 = x_1 = (-b - VD) / 2a = (-2V2 - 6) / 2 = -V2 - 3 < 0 не подходит по условию.
x_2 = x_1 + 2V2 = 3 - V2 + 2V2 = 3 + V2 > 0
p = -(3 - V2) - (3 + V2) = -3 + V2 - 3 - V2 = -6
ответ. р = -6
5.
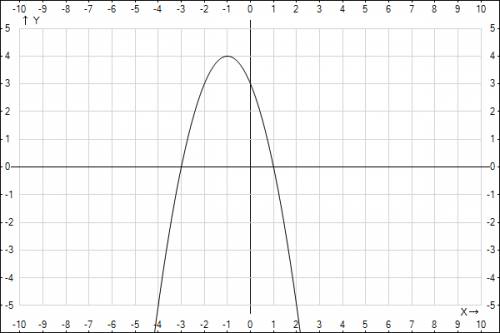
y=-x^2-2x+3,
a=-1<0 - ветви параболы вниз;
x_0=-b/(2a)=-(-2)/(2*(-1))=-1,
y_0=-(-1)^2-2*(-1)+3=4,
(-1;4) - вершина параболы;
x=0, y=3,
(0;3) - пересечение с Оу,
y=0, -x^2-2x+3=0,
x^2+2x-3=0,
по теореме Виета x_1=-3, x_2=1,
(-3;0), (1;0) - пересечения с Оx;
1) E_y=(-∞;4);
2) x∈(-1;+∞);
6.
(х^2+2х+1)(х^2-6х-16)<0,
(х^2+2х+1)(х^2-6х-16)=0,
х^2+2х+1=0, (x+1)^2=0, x+1=0, x=-1;
х^2-6х-16=0, по теореме Виета x_1=-2, x_2=8; х^2-6х-16=(x+2)(x-8);
(x+1)^2(x+2)(x-8)<0,
(x+1)^2≥0, x∈R,
(x+2)(x-8)<0,
-2<x<8,
x∈(-2;8);
7.
x^2-6bx+3b=0,
D<0,
D/4=k^2-ac=(-3b)^2-3b=3b^2-3b=3b(b-1),
3b(b-1)<0,
3b(b-1)=0,
b_1=0, b_2=1,
0<b<1,
b∈(0;1);
8.
ΔABC, уг.C=90°, CE - высота, AE=16см, BE=9см;
AB=AE+BE (по свойству сложения отрезков),
AB=16+9=25см;
AC^2=AB*AE (катет есть среднее геометрическое гипотенузы и смежного сегмента),
AC^2=25*16=400, AC=20см,
BC^2=AB*BE=25*9=225, BC=15см,
P=AB+AC+BC=25+20+15=60см.
1)5+1=6(чел)- стало в бригаде
2)6*34=204(года)- сумма возрастов шести рабочих
3)35*5=175(лет)-сумма возрастов пяти рабочих
4)204-175=29(лет) - шестому рабочему