√61
Объяснение:
Найдём производную относительно x (то есть представим выражение как функцию z с параметром y):
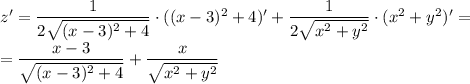
Аналогично найдём производную относительно y:
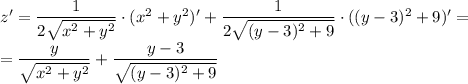
Найдём точки экстремума. Для этого обе производные должны быть одновременно равны нулю:
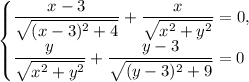
Выразим y² из первого уравнения:
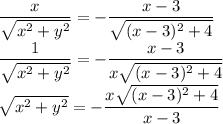
Левая часть положительна (нулём быть не может, так как она была в знаменателе), значит, и правая часть положительна:
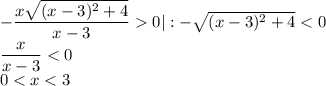
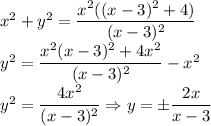
Выразим x² из второго уравнения (уравнения практически одинаковые, поэтому некоторые преобразования я опущу):
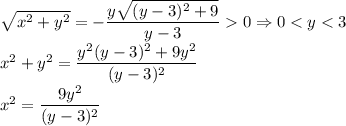
Подставим 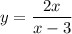 :
:
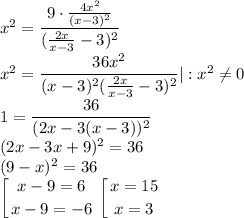
Так как 0 < x < 3, в данном случае корней нет.
Подставим 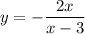 :
:
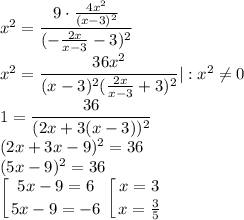
Так как 0 < x < 3, подходит только один корень 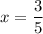 .
.
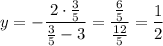 — удовлетворяет условию 0 < y < 3.
— удовлетворяет условию 0 < y < 3.
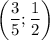 — точка экстремума.
— точка экстремума.
Исследуем знаки производной относительно x при 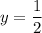 . При
. При  , например, при
, например, при 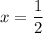 , производная имеет знак:
, производная имеет знак:
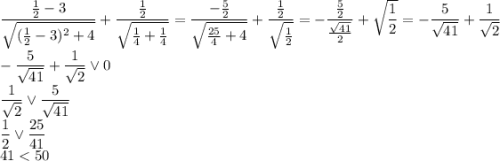
Производная имеет знак минус. При 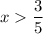 , например, при x = 1, производная имеет знак:
, например, при x = 1, производная имеет знак:
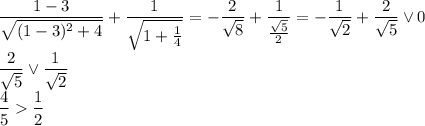
Производная имеет знак плюс. Значит, 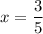 — точка минимума.
— точка минимума.
Аналогично исследуем знаки производной относительно y при 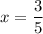 . При
. При 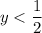 , например, при
, например, при 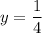 , производная имеет знак:
, производная имеет знак:
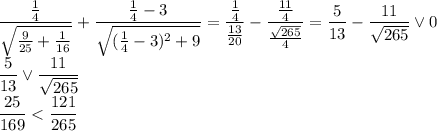
Производная имеет знак минус. При 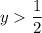 , например, при y = 1, производная имеет знак:
, например, при y = 1, производная имеет знак:
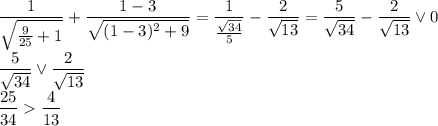
Производная имеет знак плюс. Значит, 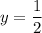 — точка минимума.
— точка минимума.
Значит, 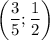 — точка минимума всей функции. Значение выражения в данной точке равно:
— точка минимума всей функции. Значение выражения в данной точке равно:
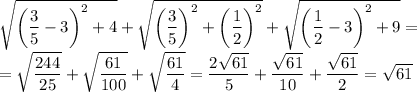
1. Линейные уравнения с двумя переменными – это уравнение вида ax+by+c=0, где x, y - переменные, a, b,c – некоторые числа.
2. Нет.
3. x - y = 8
x = 8 + y
y = x - 8
4. 2x + y = - 3
x + y/2 = - 1.5
- 2 + 0.5 = -1.5
=> Да, данная пара чисел является решением уравнения.
5. 6x - y = 12
-y = 12 - 6x
y = 6x - 12
6. Решением системы двух линейных уравнений с двумя неизвестными называют пару чисел (x,y) такую, что если подставить эти числа в уравнения системы, то каждое из уравнений системы обращается в верное равенство
7. { 5x + 7 = y - 7
{ -5x - 7 = - y + 7
8. Методом сложения.
При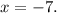
Объяснение:
Дробная функция не определена тогда, когда знаменатель её дроби равен нулю, так как на ноль делить нельзя.
То есть, чтобы функция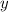 не была определена, требуется, чтобы
не была определена, требуется, чтобы 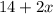 было равным нулю.
было равным нулю.