Пусть х руб -- величина исходного вклада,
а y -- процент за месяц (выраженный в целом числе)
(xy^12) руб -- получил бы гражданин через год, если бы не снимал деньги
Т.к., если бы гражданин не снимал деньги, чистый доход за год был бы 900 тысяч руб, то можно составить уравнение:
xy^12=x+900000
(xy^6-400000) руб -- сбережения в банке спустя полгода
((xy^6-400000)y^6) руб -- сбережения в банке спустя год
Т.к. всего через год гражданин получил 2 миллиона, то можно составить урвнение:
(xy^6-400000)y^6=2000000
Составляем систему уравнений: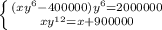
Берём второе уравнение и выражаем y^12: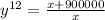
Выражаем y^6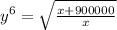
Упращаем первое выражение:
(xy^6-400000)y^6=2000000
xy^12-400000*y^6=2000000
Подстовляем второе преобразованное уравнение в первое преобразованное уравнение: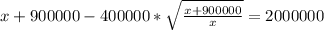
Находим х:
х=1600000
ответ: 1600000 рублей -- величина исходного вклада.
№1
а) √50 > 7
√50 > √7²
√50 > √49
б) 4√6 > 3√7
√4²*6 > √3²*7
√16*6 > √9*7
√96 > √63
№2
а) √(196 * 0,64) = √(14²*(0,8)²) = 14 * 0,8 = 11,2
б) √(72*0,5)=√36=√6² = 6
в) 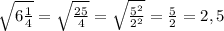
г) √(-2)⁶ = √((-2)³)²=(-2)³= - 8
№3
а) (√3+√2)² = (√3)²+ 2 *√3*√2 + (√2)²= 3 + 2√6 + 2 = 5 +2√6
б) (4 - √5)(4 + √5) = 4² - (√5)² = 16 - 5 = 11
в) 5√12 - 2√27 - 3√3 = 5√(4*3) - 2√(9*3) - 3√3 = 5√(2²*3) - 2√(3²*3) - 3√3 = 5*2√3 - 2*3√3 - 3√3= 10√3 - 6√3 - 3√3 = √3
№4
√(72*а⁵) = √(36*2 * а⁴*а)= √(6²*2 * (а²)² * а) = 6*а²*√(2а)
№5
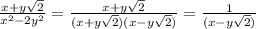
№6
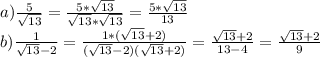
пусть изначальная сумма х руб.т.к 900тыс.прибыль за год,следовательно за 1мес. прибыль составляет 75тыс.,т.е 900000:6мес.=75000получаем,что прибыль за пол года составляет 450тыс.,т.е.6*75000=450000.но в задаче сказано,чточерез пол года ему пришлось снять со счета 400тыс.,следовательно прибыль составила всего 50тыс.,а т.к. на оставшуюся сумму по прежнему набегали проценты,то получаем,что х+50000+450000=2000000
х=1500000,по моему так.