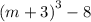
√2x-1 < √x-4.
2x-1 < x-4.
x < -4+1.
x < -3.
√2x-1 < x-2.
2x-1 < x²-4x+4.
x²-4x+4-2x+1 > 0.
x²-6x+5 > 0.
(x-1)(x-5) > 0.
x>1, x>5 и x<1, x<5.
Найдём пересечение: (-бесконечность; 1) объединение (5; +бесконечность).
√16-5x 》x-2.
16-5x 》x²-4x+4.
x²-4x+4-16+5x 《 0.
x²+x-12 《 0.
(x+4)(x-3)《 0.
x《 -4, x 》3 и x 》-4, x《 3.
Найдём пересечение: [-4;3].
a√x > 3.
√x > 3/a.
x > (3/a)².
x > 9/a².
2√x+a > x+1.
√x+a > 0,5x+0,5.
x+a > 0,25x²+0,5x+0,25.
0,25x²+0,5x+0,25-x-a > 0.
0,25x²-0,5x+0,25-a > 0.
x²-2x+2-4a > 0.
(x-1)²+1-4a > 0.
Единственное до чего смог дойти, дальше не знаю, извини.
zₓ'=((x+2y)*y²)ₓ'=(xy²+2y³)ₓ'=(xy²)ₓ'+(2y³)ₓ'=y²+0=y²
Частная производная по у (при переписывании вместо а надо писать у, в предложенных индексах нет такой буквы, потому использую а:
zₐ'=((x+2y)*y²)ₐ'=(xy²+2y³)ₐ'=(xy²)ₐ'+(2y³)ₐ'=2xy+6y²
в) zₓ'=(9(x-y²)⁴)ₓ'=9*((x-y²)⁴)ₓ'*(x-y²)ₓ'=9*4*(x-y²)³*1=36(x-y²)³
zₐ'=((9(x-y²)⁴)ₐ'=9*((x-y²)⁴)ₐ'*(x-y²)ₐ'=9*4*(x-y²)³*(-2y)=-72y(x-y²)³
б) zₓ'=(cos(2x+e^y))ₓ'=(cos(2x+e^y))ₓ'*(2x+e^y)ₓ'=-sin(2x+e^y)*2=-2sin(2x+e^y)
zₐ'=(cos(2x+e^y))ₐ'=(cos(2x+e^y)ₐ'*(2x+e^y)ₐ'=-sin(2x+e^y)*e^y