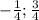Ну, я буду писать высказывание словами, а потом математически, думаю, это будет тебе полезно и понять. Итак, дано: квадрат любого числа есть число положительное. Запишем это математически (скобки для наглядности):
Отрицание первым раскрытие квантора. Существует число, квадрат которого неположителен. Математически:
Отрицание вторым я не знаю, как построить, важно, что приводит это к одному и тому же высказыванию в конце концов. Ну, а истинность установить однозначно нельзя. Если рассматривать это высказывание на множестве натуральных чисел, то оно истинно. Квадрат любого натурального числа положителен, потому что произведение двух положительных чисел положительно. А если, например, над целыми числами - то оно ложно. Контрпример: x = 0. Квадрат такого числа не является числом положительным. Если же рассматривать это высказывание над комплексными числами, найдутся и другие контрпримеры, например,
Так как дедушка родился в 20-м столетии, то первые 2 цифры года 1 и 9. Их произведение 1*9=3^2 - полный квадрат. Значит, произведение двух оставшихся цифр - тоже полный квадрат, и последняя цифра - нечётная, иначе получится четное число, то есть - не простое. Дедушка родился до 1941 года, значит, третья цифра меньше 4 (все четырёхзначные нечетные числа, первые 3 цифры которых 194 не меньше 1941). А так как произведение третьей и четвёртой цифры - полный квадрат, то эти цифры - одинаковые. Дедушка мог родиться либо в 1911, либо в 1933 году. Но 1911 - не простое число (сумма цифр делится на 3, значит и 1911 делится на 3. Остаётся 1933 - это число на самом деле простое. Дедушка родился в 1933 году.
![! \left[ \forall x \ (x^2\ \textgreater \ 0)\right] \Leftrightarrow \exists x \ (x^2 \leq 0).](/tpl/images/0564/9047/dadb8.png)
Раскрываем скобки и решаем квадратное уравнение:
ответ: