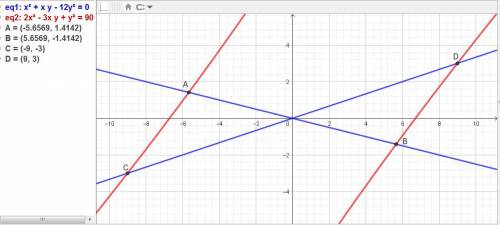
Дана система уравнений:
{x²+xy-12y²=0
{2x²-3xy+y²=90.
Первое уравнение представим так:
x²- (3xy + 4xy) + (-3y*4y) = 0.
Это равносильно разложению на множители:
(x - 3y)(x + 4y) = 0.
Отсюда выразим у = х/3 и у = -х/4, которые подставим во второе уравнение.
Подставим у = х/3.
2x² - 3x(х/3) + (х/3)² = 90,
2x²- x²+ (x²/9)=90,
10x²= 9*90
x = ± 9.
y = ± 9/3 = ± 3.
Найдены 2 корня: х1 = -9, у1 = -3, х2 = 9, у2 = 3.
Подставим у = -х/4.
2x² - 3x(-х/4) + (-x/4)² = 90,
2x²+ (3x²/4)+ (x²/16)=90,
32x² + 12x² + x²= 16*90.
45x²= 16*90
x = √32 = ±(4√2).
y = ± (4√2/4) = ± √2.
Найдены ещё 2 корня: х3 = -(4√2), у1 = √2, х4 = (4√2), у4 = -√2.
ответ: х1 = -9, у1 = -3, х2 = 9, у2 = 3.
х3 = -(4√2), у1 = √2, х4 = (4√2), у4 = -√2.
1)
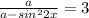
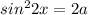
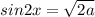
Так как значения синуса не могут быть большими единицы, получаем:
Так как выражение под радикалом и собственно весь радикал не могут быть отрицательными получаем:
Откуда получаем:
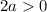
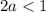
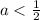
Объединяя полученные результаты получаем: a∈
ответ: a∈
2)
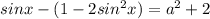
Получаем квадратное уравнение относительно t:
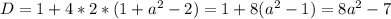
Исходя из того что данное уравнение должно иметь лишь одно решение получаем, что дискриминант должен быть равен нулю:
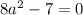
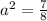
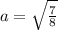
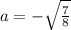
Но так как нам нужно только одно решение в заданном промежутке получаем:
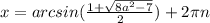
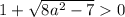
неравенство не имеет решений
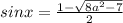
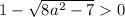
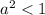
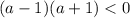
Получаем, что при a∈
данное уравнение имеет лишь один корень
ответ: a∈
ответ на фото.........