
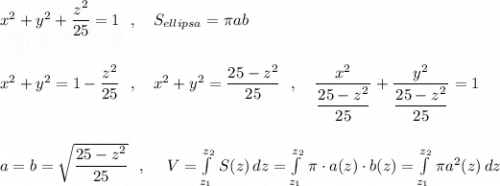
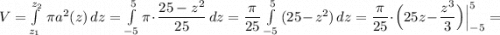
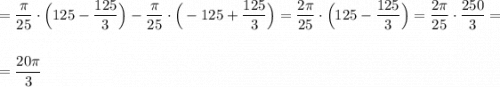
3. а). 2xy-6y^2=2y*(x-3y); б).a^3-4a=a*(a^2-4)=a*(a-2)*(a+2). 4. ВС -x см , АВ- (x+2) см, АС-2x см. уравнение: x+x+2+2x=50; x+x+2x=50-2; 4x=48; x=48/4=12(см)-ВС, 12+2=14(см)-АВ, 12*2=24(см)-АС. ответ: ВС-12 см, АВ-14 см, АС-24 см. 5. a^2-c^2-2ab+b^2-(a^2-ab-ac-ab+b^2+bc+ac-bc-c^2)=a^2-c^2-2ab+b^2-a^2+ab+ac+ab-b^2-bc-ac+bc+c^2=0. равенство доказано(все сокращается). 6.x= -y. подставляем в формулу: y=5*(-y)-8; y= -5y-8; y+5y= -8; 6y= -8, y=(-8)/6= -4/3, следовательно x=4/3. ответ: точка А (4/3: -4/3).
Этот метод мы применяли в 7-м классе для решения систем линейных уравнений. Тот алгоритм, который был выработан в 7-м классе, вполне пригоден для решения систем любых двух уравнений (не обязательно линейных) с двумя переменными х и у (разумеется, переменные могут быть обозначены и другими буквами, что не имеет значения). Фактически этим алгоритмом мы воспользовались в предыдущем параграфе, когда задача о двузначном числе привела к математической модели, представляющей собой систему уравнений. Эту систему уравнений мы решили выше методом подстановки (см. пример 1 из § 4).
Алгоритм использования метода подстановки при решении системы двух уравнений с двумя переменными х, у.
1. Выразить у через х из одного уравнения системы.
2. Подставить полученное выражение вместо у в другое уравнение системы.
3. Решить полученное уравнение относительно х.
4. Подставить поочередно каждый из найденных на третьем шаге корней уравнения вместо х в выражение у через х, полученное на первом шаге.
5. Записать ответ в виде пар значений (х; у), которые были найдены соответственно на третьем и четвертом шаге.
Переменные х и у, разумеется, равноправны, поэтому с таким же успехом мы можем на первом шаге алгоритма выразить не у через х, а х через у из одного уравнения. Обычно выбирают то уравнение, которое представляется более простым, и выражают ту переменную из него, для которой эта процедура представляется более простой.
Пример 1. Решить систему уравнений
Система уравнений
Решение.
1) Выразим х через у из первого уравнения системы: х = 5 - 3у.
2)Подставим полученное выражение вместо х во второе уравнение системы: (5 - 3у) у — 2.
3)Решим полученное уравнение:
Система уравнений
4) Подставим поочередно каждое из найденных значений у в формулу х = 5 - Зу. Если Al63.jpg то Уравнение
5) Пары (2; 1) и Al65.jpg решения заданной системы уравнений.
ответ: (2; 1); Al65.jpg
Метод алгебраического сложения
Этот метод, как и метод подстановки, знаком вам из курса алгебры 7-го класса, где он применялся для решения систем линейных уравнений. Суть метода напомним на следующем примере.
Пример 2. Решить систему уравнений
Система уравнений
Решение.
Умножим все члены первого уравнения системы на 3, а второе уравнение оставим без изменения: Система уравнений
Вычтем второе уравнение системы из ее первого уравнения:
Система уравнений
В результате алгебраического сложения двух уравнений исходной системы получилось уравнение, более простое, чем первое и второе уравнения заданной системы. Этим более простым уравнением мы имеем право заменить любое уравнение заданной системы, например второе. Тогда заданная система уравнений заменится более простой системой:
Система уравнений
Эту систему можно решить методом подстановки. Из второго уравнения находим Уравнение Подставив это выражение вместо у в первое уравнение системы, получим
Система уравнений
Осталось подставить найденные значения х в формулу Формула
Если х = 2, то
Решение
Таким образом, мы нашли два решения системы: Решение
ответ: ответ
Метод введения новых переменных
С методом введения новой переменной при решении рациональных уравнений с одной переменной вы познакомились в курсе алгебры 8-го класса. Суть этого метода при решении систем уравнений та же самая, но с технической точки зрения имеются некоторые особенности, которые мы и обсудим в следующих примерах.
Пример 3. Решить систему уравнений
Система уравнений
Решение. Введем новую переменную Al617.jpg Тогда первое уравнение системы можно будет переписать в более простом виде: Уравнение Решим это уравнение относительно переменной t: