Question

Решите систему уравнения подробно x+y+xy=7
x^2+y^2+xy=13

Answer 1

ответ: $(3;1)$,  $(1;3)$

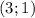Объяснение:

$\left \{ {{x+y+xy=7} \atop {x^{2} +y^{2} +xy=13}} \right.$  ⇒  $\left \{ {{x+y+xy=7} \atop {x^{2} +2xy+y^{2} -xy=13}} \right.$ ⇒ $\left \{ {{x+y+xy=7} \atop {(x+y)^{2} -xy=13}} \right.$

Сделаем замену $x+y=u;\ \ xy=v;$  Тогда:

$\left \{ {{u+v=7} \atop {u^{2} -v=13}} \right.$

Суммируем оба уравнения и получаем:

$u^{2} +u=20;\\u^{2} +u-20=0;\\D=1-4*(-20)=81=9^{2} \\u_{1} =\frac{-1+9}{2} =4;\ \ u_{2} =\frac{-1-9}{2} =-5;$

Тогда из равенства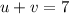 $u+v=7$ находим $v$:

$v_{1} =7-4=3;\ \ v_{2} =7-(5)=12;$

Имеем 2 системы:

$1)\ \left \{ {{u_{1} =4} \atop {v_{1} =3}} \right.$  и  $2)\ \left \{ {{u_{2} =-5} \atop {v_{2} =12}} \right.$

Подставляем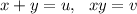 $x+y=u,\ \ xy=v$ и решаем первую систему:

$\left \{ {{x+y =4} \atop {xy =3}} \right.$ ⇒ $\left \{ {{y =4-x} \atop {x*(4-x) =3}} \right.$ ⇒

$4x-x^{2} -3=0;\\x^{2} -4x+3=0;\\D=4^{2} -4*3=4=2^{2} ;\\x_{1} =\frac{4+2}{2}=3;\ \ \ x_{2} =\frac{4-2}{2} =1$

$y_{1} =4-3=1;\ \ \ y_{2}=4-1=3;$

Имеем ответы: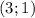 $(3;1)$  и  $(1;3)$

Решаем вторую систему:

$\left \{ {{x+y =-5} \atop {xy =12}} \right.$ ⇒ $\left \{ {{y =-5-x} \atop {x*(-5-x) =12}} \right.$ ⇒ $-5x-x^{2} -12=0$

$x^{2} +5x+12=0;\\D=5^{2} -4*12=25-48=-23$

Система решений не имеет.