отрезок длиной 24 разделён на три неравных отрезка.Рассояние между серединами крайних отрезков равно 20.Найти длинну среднего отрезка.
х/2+20+у/2=24
х+у=8
ВС=24-8=16
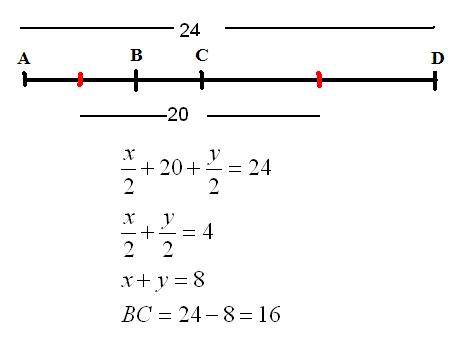
Объяснение:
график y=(∛(x+l))+m можно получить смещением графика y=∛x смещением вдоль оси OX и ОУ
1) l указывает на смещение графика вдоль оси ОХ
если график смещен вправо на l единиц то l<0
если график смещен влево на l единиц то l>0
В нашем случае график y=∛x смещен вправо на 2 единицы ⇒ l=-2
ответ l=-2
На всякий случай найдем m
2) m показывает смещение вдоль оси ОУ
если график смещен вверх на m единиц то m>0
если график смещен вниз на m единиц то m< 0
В нашем случае график y=∛x смещен вверх на 3 единицы ⇒ m=3
{ x + y = 10
{ 1/x + 1/y = 5/12
Из условия понимаем, что ни х, ни у не равны 0, так как иначе не существовало бы обратных им чисел => можно домножить вторую часть системы на ху, чтобы избавиться от дробей:
у + х = 5ху/12
Но из первой части системы мы знаем, что х + у = 10. Получаем:
5ху/12 = 10
5ху = 120
ху = 24
Вывод: x = 24/y
Совместив с первой частью изначальной системы, получаем:
24/у + у = 10
Домножим на у:
24 + у^2 = 10у
у^2 - 10у + 24 = 0
По Виету получаем, что у є {4; 6}
Из xy = 24 получаем, что х є {6; 4}
То есть, выходит два ответа: (4; 6) и (6; 4), но поскольку нам неважен порядок чисел, количество ответов сокращается до одного, и этот ответ: 4 и 6.
Пусть длины отрезков равны а, b и с. Cумма длин отрезков равна a+b+c=24. При этом сумма длин среднего и половин крайних отрезков равна a/2+b+c/2=20. Отсюда
a/2+c/2=(a+c)/2=24-20=4
a+c=4*2=8
b+8=24
b=16
ответ: длина среднего отрезка равна 16.