вторая степень
Объяснение:
Нам нужно привести многочлен к стандартному виду, а затем указать степень многочлена: а) 3/4a^2 + 3a - a.
Чтобы привести многочлен к стандартному виду сгруппируем и приведем подобные слагаемые.
Подобными называются слагаемые содержащие одинаковую буквенную часть. У нас подобными являются 3a и -a.
Сгруппируем их и приведем.
3/4a^2 + 3a - a = 3/4a^2 + a(3 - 1) = 3/4a^2 + 2a.
Нам осталось указать степень многочлена.
Степень одночлена называется наибольшая степень одночлена, который входит в многочлен.
В нашем многочлене это вторая степень
ОДЗ первого неравенства находим из условия
х-2>0⇒x>2
x+2>0⇒x>-2
Значит, ОДЗ х>2, или х∈(2;+∞), а второго
(x-2)(x+x)>0 найдем решения методом интервалов.
х=2, х=-2,
-22
+ - +
х∈(-∞;-2)∪(2;+∞)
я ВЫДЕЛИЛ Вам жирным шрифтом ОДЗ, видите разницу? Так вот применение свойства
㏒ₐx+㏒ₐy=㏒ₐ(xy) расширяет область определения на интервал
(-∞;-2)
поэтому, решая первое неравенство системы, (x-3)*(x+3)>0
-33
+ - +
Вы получите лишний промежуток, а именно (-∞;-3), входящий в интервал (-∞;-2); его надо исключить из ответа.
ответ: x∈[−3;−1,4]
Объяснение:
-4x² - 12x + 4 ≥ (x+5)²
-4x² - 12x + 4 ≥ x² + 10x + 25
-5x² - 22x - 21 ≥ 0
Теперь, решаем получившиеся уравнение как мы обычно решаем квадратные уравнения:
-5x² - 22x - 21 = 0
5x² + 22x + 21 = 0
x₁ =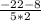 = -3
= -3
x₂ =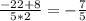
Найдя корни, решаем методом интервалов, т.е. строим числовую ось и наносим корни на нее (см. прикреп. фотографию).
x∈[−3;−1,4]