Пусть х км/ч - скорость течения реки, тогда скорость катера по течению равна (18+х) км/ч, а против течения - (18-х) км/ч. Время, затраченное на движение по течению, равно 80/(18+х); на движение против течения - 80/(18-х); на весь путь - 80/(18+х)+80/(18-х) или 9 часов. Составим и решим уравнение:
18+x
80
+
18−x
80
=9 |*(18+x)(18-x)
80(18-x)+80(18+x)=9(324-x^2)80(18−x)+80(18+x)=9(324−x
2
)
1440-80x+1440+80x=9(324-x^2)1440−80x+1440+80x=9(324−x
2
)
2880=9(324-x^2)2880=9(324−x
2
) |:9
320=324-x^2320=324−x
2
x^2=324-320x
2
=324−320
x^2=4x
2
=4
х=2
х=-2<0 (не подходит, т.к. скорость не может быть отрицательной)
ответ: скорость течения реки 2 км/ч
P.S сори что так написал(((
Раз оба корня равны нули, значит они равные. А равные корни могут быть только при дискриминанте D=0.
D=b^2-4ac a=1,b=-a^2-3a,c=3a-a^2 D=0
(-a^2-3a)^2-4(3a-a^2)=0
(a^2+3a)^2-4(3a-a^2)=0
Так и оставляем дискиминант.
x1=(-b-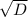 )/2a.
)/2a.
x2=(-b+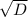 )/2a.
)/2a.
x1=x2=0, D=0
-b/2a=0
-(-a^2-3a)/2=0
a^2+3a=0
a(a+3)=0
a=0 или a=-3.
Теперь проверяем, удолетворяет ли найденные нами a решению уравнения с параметром. Для этого подставим их в уравнение дискриминанта:
(a^2+3a)^2-4(3a-a^2)=0
(0+0)^2-4(0-0)=0
0=0
a=0 - удолетворяет
(9-9)^2-4(-9-9)=0
72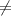 0
0
a=-3 - не удолетворяет условию.
ответ: 0.