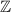 разделим на три класса:
разделим на три класса: , где + обозначает операцию объединения и изначает, что множества
, где + обозначает операцию объединения и изначает, что множества 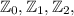 дисъюнктны.
дисъюнктны.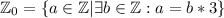
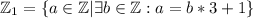

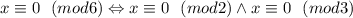
 .
.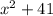 делится на два (сумма нечетных чисел четна), то есть выражение все равно делится на два, первое условие выполнено. Докажем, что x делится на 3:
делится на два (сумма нечетных чисел четна), то есть выражение все равно делится на два, первое условие выполнено. Докажем, что x делится на 3: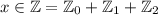 , то рассмотрим три случая:
, то рассмотрим три случая: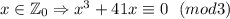 так как
так как 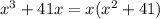 .
.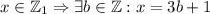
 для каких-то
для каких-то  , то есть
, то есть 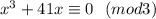 .
.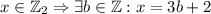 .
.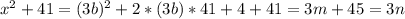 для каких-то
для каких-то  , то есть
, то есть 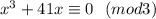 .
.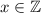 выражение
выражение 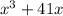 делится на 6.
делится на 6.
Задание 1.
-8
Задание 2.
x∈[0; 4]
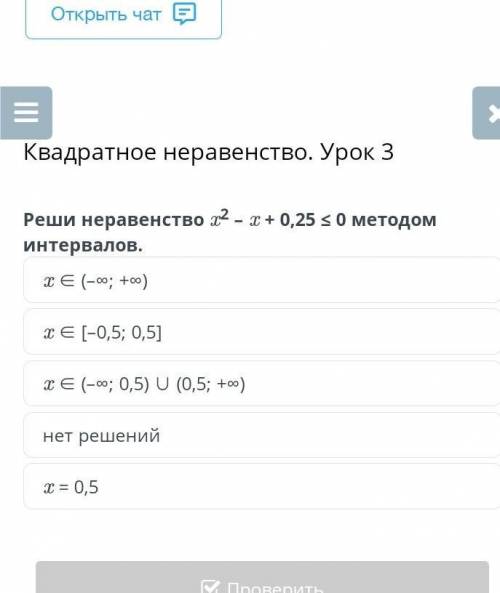
Задание 3.
x=0,5
Задание 4.
6
Задание 5.
1-3
2-4
3-1
4-2
Задание 6.
Задание 7.
1-4
2-1
3-2
4-3
Задание 8.
1
Задание 9.
x∈(-∞; -0,5)∪(8; +∞)
:
1. Поставь 5 звёзд.
2. Поставь .
3. Сделай лучшим ответом.